Edit: Shortly after posting this, I found where the machinery I develop here was discussed in the literature. Real Algebraic Geometry by Bochnak, Coste, and Roy covers at least most of this material. I may eventually edit this to clean it up and adopt more standard notation, but don’t hold your breath.
Introduction
In algebraic geometry, an affine algebraic set is a subset of ![]() which is the set of solutions to some finite set of polynomials. Since all ideals of
which is the set of solutions to some finite set of polynomials. Since all ideals of ![]() are finitely generated, this is equivalent to saying that an affine algebraic set is a subset of
are finitely generated, this is equivalent to saying that an affine algebraic set is a subset of ![]() which is the set of solutions to some arbitrary set of polynomials.
which is the set of solutions to some arbitrary set of polynomials.
In semialgebraic geometry, a closed semialgebraic set is a subset of ![]() of the form
of the form ![]() for some finite set of polynomials
for some finite set of polynomials ![]() . Unlike in the case of affine algebraic sets, if
. Unlike in the case of affine algebraic sets, if ![]() is an arbitrary set of polynomials,
is an arbitrary set of polynomials, ![]() is not necessarily a closed semialgebraic set. As a result of this, the collection of closed semialgebraic sets are not the closed sets of a topology on
is not necessarily a closed semialgebraic set. As a result of this, the collection of closed semialgebraic sets are not the closed sets of a topology on ![]() . In the topology on
. In the topology on ![]() generated by closed semialgebraic sets being closed, the closed sets are the sets of the form
generated by closed semialgebraic sets being closed, the closed sets are the sets of the form ![]() for arbitrary
for arbitrary ![]() . Semialgebraic geometry usually restricts itself to the study of semialgebraic sets, but here I wish to consider all the closed sets of this topology. Notice that closed semialgebraic sets are also closed in the standard topology, so the standard topology is a refinement of this one. Notice also that the open ball
. Semialgebraic geometry usually restricts itself to the study of semialgebraic sets, but here I wish to consider all the closed sets of this topology. Notice that closed semialgebraic sets are also closed in the standard topology, so the standard topology is a refinement of this one. Notice also that the open ball ![]() of radius
of radius ![]() centered at
centered at ![]() is the complement of the closed semialgebraic set
is the complement of the closed semialgebraic set ![]() , and these open balls are a basis for the standard topology, so this topology is a refinement of the standard one. Thus, the topology I have defined is exactly the standard topology on
, and these open balls are a basis for the standard topology, so this topology is a refinement of the standard one. Thus, the topology I have defined is exactly the standard topology on ![]() .
.
In algebra, instead of referring to a set of polynomials, it is often nicer to talk about the ideal generated by that set instead. What is the analog of an ideal in ordered algebra? It’s this thing:
Definition: If ![]() is a partially ordered commutative ring, a cone
is a partially ordered commutative ring, a cone ![]() in
in ![]() is a subsemiring of
is a subsemiring of ![]() which contains all positive elements, and such that
which contains all positive elements, and such that ![]() is an ideal of
is an ideal of ![]() . By “subsemiring”, I mean a subset that contains
. By “subsemiring”, I mean a subset that contains ![]() and
and ![]() , and is closed under addition and multiplication (but not necessarily negation). If
, and is closed under addition and multiplication (but not necessarily negation). If ![]() , the cone generated by
, the cone generated by ![]() , denoted
, denoted ![]() , is the smallest cone containing
, is the smallest cone containing ![]() . Given a cone
. Given a cone ![]() , the ideal
, the ideal ![]() will be called the interior ideal of
will be called the interior ideal of ![]() , and denoted
, and denoted ![]() .
.
![]() is partially ordered by
is partially ordered by ![]() . If
. If ![]() is a set of polynomials and
is a set of polynomials and ![]() , then
, then ![]() . Thus I can consider closed sets to be defined by cones. We now have a Galois connection between cones of
. Thus I can consider closed sets to be defined by cones. We now have a Galois connection between cones of ![]() and subsets of
and subsets of ![]() , given by, for a cone
, given by, for a cone ![]() , its positive-set is
, its positive-set is ![]() (I’m calling it the “positive-set” even though it is where the polynomials are all non-negative, because “non-negative-set” is kind of a mouthful), and for
(I’m calling it the “positive-set” even though it is where the polynomials are all non-negative, because “non-negative-set” is kind of a mouthful), and for ![]() , its cone is
, its cone is ![]() .
. ![]() is closure in the standard topology on
is closure in the standard topology on ![]() (the analog in algebraic geometry is closure in the Zariski topology on
(the analog in algebraic geometry is closure in the Zariski topology on ![]() ). A closed set
). A closed set ![]() is semialgebraic if and only if it is the positive-set of a finitely-generated cone.
is semialgebraic if and only if it is the positive-set of a finitely-generated cone.
Quotients by cones, and coordinate rings
An affine algebraic set ![]() is associated with its coordinate ring
is associated with its coordinate ring ![]() . We can do something analogous for closed subsets of
. We can do something analogous for closed subsets of ![]() .
.
Definition: If ![]() is a partially ordered commutative ring and
is a partially ordered commutative ring and ![]() is a cone,
is a cone, ![]() is the ring
is the ring ![]() , equipped with the partial order given by
, equipped with the partial order given by ![]() if and only if
if and only if ![]() , for
, for ![]() .
.
Definition: If ![]() is closed, the coordinate ring of
is closed, the coordinate ring of ![]() is
is ![]() . This is the ring of functions
. This is the ring of functions ![]() that are restrictions of polynomials, ordered by
that are restrictions of polynomials, ordered by ![]() if and only if
if and only if ![]() . For arbitrary
. For arbitrary ![]() , the ring of regular functions on
, the ring of regular functions on ![]() , denoted
, denoted ![]() , consists of functions on
, consists of functions on ![]() that are locally ratios of polynomials, again ordered by
that are locally ratios of polynomials, again ordered by ![]() if and only if
if and only if ![]() . Assigning its ring of regular functions to each open subset of
. Assigning its ring of regular functions to each open subset of ![]() endows
endows ![]() with a sheaf of partially ordered commutative rings.
with a sheaf of partially ordered commutative rings.
For closed ![]() ,
, ![]() , and this inclusion is generally proper, both because it is possible to divide by polynomials that do not have roots in
, and this inclusion is generally proper, both because it is possible to divide by polynomials that do not have roots in ![]() , and because
, and because ![]() may be disconnected, making it possible to have functions given by different polynomials on different connected components.
may be disconnected, making it possible to have functions given by different polynomials on different connected components.
Positivstellensätze
What is ![]() ? The Nullstellensatz says that its analog in algebraic geometry is the radical of an ideal. As such, we could say that the radical of a cone
? The Nullstellensatz says that its analog in algebraic geometry is the radical of an ideal. As such, we could say that the radical of a cone ![]() , denoted
, denoted ![]() , is
, is ![]() , and that a cone
, and that a cone ![]() is radical if
is radical if ![]() . In algebraic geometry, the Nullstellensatz shows that a notion of radical ideal defined without reference to algebraic sets in fact characterizes the ideals which are closed in the corresponding Galois connection. It would be nice to have a description of the radical of a cone that does not refer to the Galois connection. There is a semialgebraic analog of the Nullstellensatz, but it does not quite characterize radical cones.
. In algebraic geometry, the Nullstellensatz shows that a notion of radical ideal defined without reference to algebraic sets in fact characterizes the ideals which are closed in the corresponding Galois connection. It would be nice to have a description of the radical of a cone that does not refer to the Galois connection. There is a semialgebraic analog of the Nullstellensatz, but it does not quite characterize radical cones.
Positivstellensatz 1: If ![]() is a finitely-generated cone and
is a finitely-generated cone and ![]() is a polynomial, then
is a polynomial, then ![]() if and only if
if and only if ![]() such that
such that ![]() .
.
There are two ways in which this is unsatisfactory: first, it applies only to finitely-generated cones, and second, it tells us exactly which polynomials are strictly positive everywhere on a closed semialgebraic set, whereas we want to know which polynomials are non-negative everywhere on a set.
The second problem is easier to handle: a polynomial ![]() is non-negative everywhere on a set
is non-negative everywhere on a set ![]() if and only if there is a decreasing sequence of polynomials
if and only if there is a decreasing sequence of polynomials ![]() converging to
converging to ![]() such that each
such that each ![]() is strictly positive everywhere on
is strictly positive everywhere on ![]() . Thus, to find
. Thus, to find ![]() , it is enough to first find all the polynomials that are strictly positive everywhere on
, it is enough to first find all the polynomials that are strictly positive everywhere on ![]() , and then take the closure under lower limits. Thus we have a characterization of radicals of finitely-generated cones.
, and then take the closure under lower limits. Thus we have a characterization of radicals of finitely-generated cones.
Positivstellensatz 2: If ![]() is a finitely-generated cone,
is a finitely-generated cone, ![]() is the closure of
is the closure of ![]() , where the closure of a subset
, where the closure of a subset ![]() is defined to be the set of all polynomials in
is defined to be the set of all polynomials in ![]() which are infima of chains contained in
which are infima of chains contained in ![]() .
.
This still doesn’t even tell us what’s going on for cones which are not finitely-generated. However, we can generalize the Positivstellensatz to some other cones.
Positivstellensatz 3: Let ![]() be a cone containing a finitely-generated subcone
be a cone containing a finitely-generated subcone ![]() such that
such that ![]() is compact. If
is compact. If ![]() is a polynomial, then
is a polynomial, then ![]() if and only if
if and only if ![]() such that
such that ![]() . As before, it follows that
. As before, it follows that ![]() is the closure of
is the closure of ![]() .
.
proof: For a given ![]() ,
, ![]() , an intersection of closed sets contained in the compact set
, an intersection of closed sets contained in the compact set ![]() , which is thus empty if and only if some finite subcollection of them has empty intersection within
, which is thus empty if and only if some finite subcollection of them has empty intersection within ![]() . Thus if
. Thus if ![]() is strictly positive everywhere on
is strictly positive everywhere on ![]() , then there is some finitely generated subcone
, then there is some finitely generated subcone ![]() such that
such that ![]() is strictly positive everywhere on
is strictly positive everywhere on ![]() , and
, and ![]() is finitely-generated, so by Positivstellensatz 1, there is
is finitely-generated, so by Positivstellensatz 1, there is ![]() such that
such that ![]() .
. ![]()
For cones that are not finitely-generated and do not contain any finitely-generated subcones with compact positive-sets, the Positivstellensatz will usually fail. Thus, it seems likely that if there is a satisfactory general definition of radical for cones in arbitrary partially ordered commutative rings that agrees with this one in ![]() , then there is also an abstract notion of “having a compact positive-set” for such cones, even though they don’t even have positive-sets associated with them.
, then there is also an abstract notion of “having a compact positive-set” for such cones, even though they don’t even have positive-sets associated with them.
Beyond 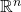
An example of cone for which the Positivstellensatz fails is ![]() , the cone of polynomials that are non-negative on sufficiently large inputs (equivalently, the cone of polynomials that are either
, the cone of polynomials that are non-negative on sufficiently large inputs (equivalently, the cone of polynomials that are either ![]() or have positive leading coefficient).
or have positive leading coefficient). ![]() , and
, and ![]() is strictly positive on
is strictly positive on ![]() , but for
, but for ![]() ,
, ![]() .
.
However, it doesn’t really look ![]() is trying to point to the empty set; instead,
is trying to point to the empty set; instead, ![]() is trying to describe the set of all infinitely large reals, which only looks like the empty set because there are no infinitely large reals. Similar phenomena can occur even for cones that do contain finitely-generated subcones with compact positive-sets. For example, let
is trying to describe the set of all infinitely large reals, which only looks like the empty set because there are no infinitely large reals. Similar phenomena can occur even for cones that do contain finitely-generated subcones with compact positive-sets. For example, let ![]() .
. ![]() , but
, but ![]() is trying to point out the set containing
is trying to point out the set containing ![]() and all positive infinitesimals. Since
and all positive infinitesimals. Since ![]() has no infinitesimals, this looks like
has no infinitesimals, this looks like ![]() .
.
To formalize this intuition, we can change the Galois connection. We could say that for a cone ![]() ,
, ![]() , where
, where ![]() is the field of hyperreals. All you really need to know about
is the field of hyperreals. All you really need to know about ![]() is that it is a big ordered field extension of
is that it is a big ordered field extension of ![]() .
. ![]() is the set of hyperreals that are bigger than any real number, and
is the set of hyperreals that are bigger than any real number, and ![]() is the set of hyperreals that are non-negative and smaller than any positive real. The cone of a subset
is the set of hyperreals that are non-negative and smaller than any positive real. The cone of a subset ![]() , denoted
, denoted ![]() will be defined as before, still consisting only of polynomials with real coefficients. This defines a topology on
will be defined as before, still consisting only of polynomials with real coefficients. This defines a topology on ![]() by saying that the closed sets are the fixed points of
by saying that the closed sets are the fixed points of ![]() . This topology is not
. This topology is not ![]() because, for example, there are many hyperreals that are larger than all reals, and they cannot be distinguished by polynomials with real coefficients. There is no use keeping track of the difference between points that are in the same closed sets. If you have a topology that is not
because, for example, there are many hyperreals that are larger than all reals, and they cannot be distinguished by polynomials with real coefficients. There is no use keeping track of the difference between points that are in the same closed sets. If you have a topology that is not ![]() , you can make it
, you can make it ![]() by identifying any pair of points that have the same closure. If we do this to
by identifying any pair of points that have the same closure. If we do this to ![]() , we get what I’m calling ordered affine
, we get what I’m calling ordered affine ![]() -space over
-space over ![]() .
.
Definition: An ![]() -type over
-type over ![]() is a set
is a set ![]() of inequalities, consisting of, for each polynomial
of inequalities, consisting of, for each polynomial ![]() , one of the inequalities
, one of the inequalities ![]() or
or ![]() , such that there is some totally ordered field extension
, such that there is some totally ordered field extension ![]() and
and ![]() such that all inequalities in
such that all inequalities in ![]() are true about
are true about ![]() .
. ![]() is called the type of
is called the type of ![]() . Ordered affine
. Ordered affine ![]() -space over
-space over ![]() , denoted
, denoted ![]() is the set of
is the set of ![]() -types over
-types over ![]() .
.
Compactness Theorem: Let ![]() be a set of inequalities consisting of, for each polynomial
be a set of inequalities consisting of, for each polynomial ![]() , one of the inequalities
, one of the inequalities ![]() or
or ![]() . Then
. Then ![]() is an
is an ![]() -type if and only if for any finite subset
-type if and only if for any finite subset ![]() , there is
, there is ![]() such that all inequalities in
such that all inequalities in ![]() are true about
are true about ![]() .
.
proof: Follows from the compactness theorem of first-order logic and the fact that ordered field extensions of ![]() embed into elementary extensions of
embed into elementary extensions of ![]() . The theorem is not obvious if you do not know what those mean.
. The theorem is not obvious if you do not know what those mean. ![]()
An ![]() -type represents an
-type represents an ![]() -tuple of elements of an ordered field extension of
-tuple of elements of an ordered field extension of ![]() , up to the equivalence relation that identifies two such tuples that relate to
, up to the equivalence relation that identifies two such tuples that relate to ![]() by polynomials in the same way. One way that a tuple of elements of an extension of
by polynomials in the same way. One way that a tuple of elements of an extension of ![]() can relate to elements of
can relate to elements of ![]() is to equal a tuple of elements of
is to equal a tuple of elements of ![]() , so there is a natural inclusion
, so there is a natural inclusion ![]() that associates an
that associates an ![]() -tuple of reals with the set of polynomial inequalities that are true at that
-tuple of reals with the set of polynomial inequalities that are true at that ![]() -tuple.
-tuple.
A tuple of polynomials ![]() describes a function
describes a function ![]() , which extends naturally to a function
, which extends naturally to a function ![]() by
by ![]() is the type of
is the type of ![]() , where
, where ![]() is an
is an ![]() -tuple of elements of type
-tuple of elements of type ![]() in an extension of
in an extension of ![]() . In particular, a polynomial
. In particular, a polynomial ![]() extends to a function
extends to a function ![]() , and
, and ![]() is totally ordered by
is totally ordered by ![]() if and only if
if and only if ![]() , where
, where ![]() and
and ![]() are elements of type
are elements of type ![]() and
and ![]() , respectively, in an extension of
, respectively, in an extension of ![]() .
. ![]() if and only if
if and only if ![]() , so we can talk about inequalities satisfied by types in place of talking about inequalities contained in types.
, so we can talk about inequalities satisfied by types in place of talking about inequalities contained in types.
I will now change the Galois connection that we are talking about yet again (last time, I promise). It will now be a Galois connection between the set of cones in ![]() and the set of subsets of
and the set of subsets of ![]() . For a cone
. For a cone ![]() ,
, ![]() . For a set
. For a set ![]() ,
, ![]() . Again, this defines a topology on
. Again, this defines a topology on ![]() by saying that fixed points of
by saying that fixed points of ![]() are closed.
are closed. ![]() is
is ![]() ; in fact, it is the
; in fact, it is the ![]() topological space obtained from
topological space obtained from ![]() by identifying points with the same closure as mentioned earlier.
by identifying points with the same closure as mentioned earlier. ![]() is also compact, as can be seen from the compactness theorem.
is also compact, as can be seen from the compactness theorem. ![]() is not
is not ![]() (unless
(unless ![]() ). Note that model theorists have their own topology on
). Note that model theorists have their own topology on ![]() , which is distinct from the one I use here, and is a refinement of it.
, which is distinct from the one I use here, and is a refinement of it.
The new Galois connection is compatible with the old one via the inclusion ![]() , in the sense that if
, in the sense that if ![]() , then
, then ![]() (where we identify
(where we identify ![]() with its image in
with its image in ![]() ), and for a cone
), and for a cone ![]() ,
, ![]() .
.
Like our intermediate Galois connection ![]() , our final Galois connection
, our final Galois connection ![]() succeeds in distinguishing
succeeds in distinguishing ![]() and
and ![]() from
from ![]() and
and ![]() , respectively, in the desirable manner.
, respectively, in the desirable manner. ![]() consists of the type of numbers larger than any real, and
consists of the type of numbers larger than any real, and ![]() consists of the types of
consists of the types of ![]() and of positive numbers smaller than any positive real.
and of positive numbers smaller than any positive real.
Just like for subsets of ![]() , a closed subset
, a closed subset ![]() has a coordinate ring
has a coordinate ring ![]() , and an arbitrary
, and an arbitrary ![]() has a ring of regular functions
has a ring of regular functions ![]() consisting of functions on
consisting of functions on ![]() that are locally ratios of polynomials, ordered by
that are locally ratios of polynomials, ordered by ![]() if and only if
if and only if ![]() , where
, where ![]() is a representation of
is a representation of ![]() as a ratio of polynomials in a neighborhood of
as a ratio of polynomials in a neighborhood of ![]() , either
, either ![]() and
and ![]() , or
, or ![]() and
and ![]() , and
, and ![]() if and only if
if and only if ![]() . As before,
. As before, ![]() for closed
for closed ![]() .
.
![]() is analogous to
is analogous to ![]() from algebraic geometry because if, in the above definitions, you replace “
from algebraic geometry because if, in the above definitions, you replace “![]() ” and “
” and “![]() ” with “
” with “![]() ” and “
” and “![]() “, replace totally ordered field extensions with field extensions, and replace cones with ideals, then you recover a description of
“, replace totally ordered field extensions with field extensions, and replace cones with ideals, then you recover a description of ![]() , in the sense of
, in the sense of ![]() .
.
What about an analog of projective space? Since we’re paying attention to order, we should look at spheres, not real projective space. The ![]() -sphere over
-sphere over ![]() , denoted
, denoted ![]() , can be described as the locus of
, can be described as the locus of ![]() in
in ![]() .
.
For any totally ordered field ![]() , we can define
, we can define ![]() similarly to
similarly to ![]() , as the space of
, as the space of ![]() -types over
-types over ![]() , defined as above, replacing
, defined as above, replacing ![]() with
with ![]() (although a model theorist would no longer call it the space of
(although a model theorist would no longer call it the space of ![]() -types over
-types over ![]() ). The compactness theorem is not true for arbitrary
). The compactness theorem is not true for arbitrary ![]() , but its corollary that
, but its corollary that ![]() is compact still is true.
is compact still is true.
Visualizing 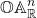 and
and 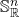
![]() should be thought of as the
should be thought of as the ![]() -sphere with infinitesimals in all directions around each point. Specifically,
-sphere with infinitesimals in all directions around each point. Specifically, ![]() is just
is just ![]() , a pair of points. The closed points of
, a pair of points. The closed points of ![]() are the points of
are the points of ![]() , and for each closed point
, and for each closed point ![]() , there is an
, there is an ![]() -sphere of infinitesimals around
-sphere of infinitesimals around ![]() , meaning a copy of
, meaning a copy of ![]() , each point of which has
, each point of which has ![]() in its closure.
in its closure.
![]() should be thought of as
should be thought of as ![]() -space with infinitesimals in all directions around each point, and infinities in all directions. Specifically,
-space with infinitesimals in all directions around each point, and infinities in all directions. Specifically, ![]() contains
contains ![]() , and for each point
, and for each point ![]() , there is an
, there is an ![]() -sphere of infinitesimals around
-sphere of infinitesimals around ![]() , and there is also a copy of
, and there is also a copy of ![]() around the whole thing, the closed points of which are limits of rays in
around the whole thing, the closed points of which are limits of rays in ![]() .
.
![]() and
and ![]() relate to each other the same way that
relate to each other the same way that ![]() and
and ![]() do. If you remove a closed point from
do. If you remove a closed point from ![]() , you get
, you get ![]() , where the sphere of infinitesimals around the removed closed point becomes the sphere of infinities of
, where the sphere of infinitesimals around the removed closed point becomes the sphere of infinities of ![]() .
.
More generally, if ![]() is a totally ordered field, let
is a totally ordered field, let ![]() be its real closure.
be its real closure. ![]() consists of the Cauchy completion of
consists of the Cauchy completion of ![]() (as a metric space with distances valued in
(as a metric space with distances valued in ![]() ), and for each point
), and for each point ![]() (though not for points that are limits of Cauchy sequences that do not converge in
(though not for points that are limits of Cauchy sequences that do not converge in ![]() ), an
), an ![]() -sphere
-sphere ![]() of infinitesimals around
of infinitesimals around ![]() , and an
, and an ![]() -sphere
-sphere ![]() around the whole thing, where
around the whole thing, where ![]() is the locus of
is the locus of ![]() in
in ![]() .
. ![]() does not distinguish between fields with the same real closure.
does not distinguish between fields with the same real closure.
More Positivstellensätze
This Galois connection gives us a new notion of what it means for a cone to be radical, which is distinct from the old one and is better, so I will define ![]() to be
to be ![]() . A cone
. A cone ![]() will be called radical if
will be called radical if ![]() . Again, it would be nice to be able to characterize radical cones without referring to the Galois connection. And this time, I can do it. Note that since
. Again, it would be nice to be able to characterize radical cones without referring to the Galois connection. And this time, I can do it. Note that since ![]() is compact, the proof of Positivstellensatz 3 shows that in our new context, the Positivstellensatz holds for all cones, since even the subcone generated by
is compact, the proof of Positivstellensatz 3 shows that in our new context, the Positivstellensatz holds for all cones, since even the subcone generated by ![]() has a compact positive-set.
has a compact positive-set.
Positivstellensatz 4: If ![]() is a cone and
is a cone and ![]() is a polynomial, then
is a polynomial, then ![]() if and only if
if and only if ![]() such that
such that ![]() .
.
However, we can no longer add in lower limits of sequences of polynomials. For example, ![]() for all real
for all real ![]() , but
, but ![]() , even though
, even though ![]() is radical. This happens because, where
is radical. This happens because, where ![]() is the type of positive infinitesimals,
is the type of positive infinitesimals, ![]() for real
for real ![]() , but
, but ![]() . However, we can add in lower limits of sequences contained in finitely-generated subcones, and this is all we need to add, so this characterizes radical cones.
. However, we can add in lower limits of sequences contained in finitely-generated subcones, and this is all we need to add, so this characterizes radical cones.
Positivstellensatz 5: If ![]() is a cone,
is a cone, ![]() is the union over all finitely-generated subcones
is the union over all finitely-generated subcones ![]() of the closure of
of the closure of ![]() (again the closure of a subset
(again the closure of a subset ![]() is defined to be the set of all polynomials in
is defined to be the set of all polynomials in ![]() which are infima of chains contained in
which are infima of chains contained in ![]() ).
).
Proof: Suppose ![]() is a subcone generated by a finite set
is a subcone generated by a finite set ![]() , and
, and ![]() is the infimum of a chain
is the infimum of a chain ![]() . For any
. For any ![]() , if
, if ![]() for each
for each ![]() , then
, then ![]() for each
for each ![]() , and hence
, and hence ![]() . That is, the finite set of inequalities
. That is, the finite set of inequalities ![]() does not hold anywhere in
does not hold anywhere in ![]() . By the compactness theorem, there are no
. By the compactness theorem, there are no ![]() -types satisfying all those inequalities. Given
-types satisfying all those inequalities. Given ![]() ,
, ![]() , so
, so ![]() ; that is,
; that is, ![]() .
.
Conversely, suppose ![]() . Then by the compactness theorem, there are some
. Then by the compactness theorem, there are some ![]() such that
such that ![]() . Then
. Then ![]() ,
, ![]() is strictly positive on
is strictly positive on ![]() , and hence by Positivstellensatz 4,
, and hence by Positivstellensatz 4, ![]() such that
such that ![]() . That is,
. That is, ![]() is a chain contained in
is a chain contained in ![]() , a finitely-generated subcone of
, a finitely-generated subcone of ![]() , whose infimum is
, whose infimum is ![]() .
. ![]()
Ordered commutative algebra
Even though they are technically not isomorphic, ![]() and
and ![]() are closely related, and can often be used interchangeably. Of the two,
are closely related, and can often be used interchangeably. Of the two, ![]() is of a form that can be more easily generalized to more abstruse situations in algebraic geometry, which may indicate that it is the better thing to talk about, whereas
is of a form that can be more easily generalized to more abstruse situations in algebraic geometry, which may indicate that it is the better thing to talk about, whereas ![]() is merely the simpler thing that is easier to think about and just as good in practice in many contexts. In contrast,
is merely the simpler thing that is easier to think about and just as good in practice in many contexts. In contrast, ![]() and
and ![]() are different in important ways. The situation in algebraic geometry provides further reason to pay more attention to
are different in important ways. The situation in algebraic geometry provides further reason to pay more attention to ![]() than to
than to ![]() .
.
The next thing to look for would be an analog of the spectrum of a ring for a partially ordered commutative ring (I will henceforth abbreviate “partially ordered commutative ring” as “ordered ring” in order to cut down on the profusion of adjectives) in a way that makes use of the order, and gives us ![]() when applied to
when applied to ![]() . I will call it the order spectrum of an ordered ring
. I will call it the order spectrum of an ordered ring ![]() , denoted
, denoted ![]() . Then of course
. Then of course ![]() can be defined as
can be defined as ![]() .
. ![]() should be, of course, the set of prime cones. But what even is a prime cone?
should be, of course, the set of prime cones. But what even is a prime cone?
Definition: A cone ![]() is prime if
is prime if ![]() is a totally ordered integral domain.
is a totally ordered integral domain.
Definition: ![]() is the set of prime cones in
is the set of prime cones in ![]() , equipped with the topology whose closed sets are the sets of prime cones containing a given cone.
, equipped with the topology whose closed sets are the sets of prime cones containing a given cone.
An ![]() -type
-type ![]() can be seen as a cone, by identifying it with
can be seen as a cone, by identifying it with ![]() , aka
, aka ![]() . Under this identification,
. Under this identification, ![]() , as desired. The prime cones in
, as desired. The prime cones in ![]() are also the radical cones
are also the radical cones ![]() such that
such that ![]() is irreducible. Notice that irreducible subsets of
is irreducible. Notice that irreducible subsets of ![]() are much smaller than irreducible subsets of
are much smaller than irreducible subsets of ![]() ; in particular, none of them contain more than one element of
; in particular, none of them contain more than one element of ![]() .
.
There is also a natural notion of maximal cone.
Definition: A cone ![]() is maximal if
is maximal if ![]() and there are no strictly intermediate cones between
and there are no strictly intermediate cones between ![]() and
and ![]() . Equivalently, if
. Equivalently, if ![]() is prime and closed in
is prime and closed in ![]() .
.
Maximal ideals of ![]() correspond to elements of
correspond to elements of ![]() . And the cones of elements of
. And the cones of elements of ![]() are maximal cones in
are maximal cones in ![]() , but unlike in the complex case, these are not all the maximal cones, since there are closed points in
, but unlike in the complex case, these are not all the maximal cones, since there are closed points in ![]() outside of
outside of ![]() . For example,
. For example, ![]() is a maximal cone, and the type of numbers greater than all reals is closed. To characterize the cones of elements of
is a maximal cone, and the type of numbers greater than all reals is closed. To characterize the cones of elements of ![]() , we need something slightly different.
, we need something slightly different.
Definition: A cone ![]() is ideally maximal if
is ideally maximal if ![]() is a totally ordered field. Equivalently, if
is a totally ordered field. Equivalently, if ![]() is maximal and
is maximal and ![]() is a maximal ideal.
is a maximal ideal.
Elements of ![]() correspond to ideally maximal cones of
correspond to ideally maximal cones of ![]() .
.
![]() also allows us to define the radical of a cone in an arbitrary partially ordered commutative ring.
also allows us to define the radical of a cone in an arbitrary partially ordered commutative ring.
Definition: For a cone ![]() ,
, ![]() is the intersection of all prime cones containing
is the intersection of all prime cones containing ![]() .
. ![]() is radical if
is radical if ![]() .
.
Conjecture: ![]() is the union over all finitely-generated subcones
is the union over all finitely-generated subcones ![]() of the closure of
of the closure of ![]() (as before, the closure of a subset
(as before, the closure of a subset ![]() is defined to be the set of all elements of
is defined to be the set of all elements of ![]() which are infima of chains contained in
which are infima of chains contained in ![]() ).
).
Order schemes
Definition: An ordered ringed space is a topological space equipped with a sheaf of ordered rings. An ordered ring is local if it has a unique ideally maximal cone, and a locally ordered ringed space is an ordered ringed space whose stalks are local.
![]() can be equipped with a sheaf of ordered rings
can be equipped with a sheaf of ordered rings ![]() , making it a locally ordered ringed space.
, making it a locally ordered ringed space.
Definition: For a prime cone ![]() , the localization of
, the localization of ![]() at
at ![]() , denoted
, denoted ![]() , is the ring
, is the ring ![]() equipped with an ordering that makes it a local ordered ring. This will be the stalk at
equipped with an ordering that makes it a local ordered ring. This will be the stalk at ![]() of
of ![]() . A fraction
. A fraction ![]() (
(![]() ) is also an element of
) is also an element of ![]() for any prime cone
for any prime cone ![]() whose interior ideal does not contain
whose interior ideal does not contain ![]() . This is an open neighborhood of
. This is an open neighborhood of ![]() (its complement is the set of prime cones containing
(its complement is the set of prime cones containing ![]() ). There is a natural map
). There is a natural map ![]() given by
given by ![]() , and the total order on
, and the total order on ![]() extends uniquely to a total order on the fraction field, so for
extends uniquely to a total order on the fraction field, so for ![]() , we can say that
, we can say that ![]() at
at ![]() if this is true of their images in
if this is true of their images in ![]() . We can then say that
. We can then say that ![]() near
near ![]() if
if ![]() at every point in some neighborhood of
at every point in some neighborhood of ![]() , which defines the ordering on
, which defines the ordering on ![]() .
.
Definition: For open ![]() ,
, ![]() consists of elements of
consists of elements of ![]() that are locally ratios of elements of
that are locally ratios of elements of ![]() .
. ![]() is ordered by
is ordered by ![]() if and only if
if and only if ![]()
![]() near
near ![]() (equivalently, if
(equivalently, if ![]()
![]() at
at ![]() ).
).
![]() , and this inclusion can be proper. Conjecture:
, and this inclusion can be proper. Conjecture: ![]() as locally ordered ringed spaces for open
as locally ordered ringed spaces for open ![]() . This conjecture says that it makes sense to talk about whether or not a locally ordered ringed space looks locally like an order spectrum near a given point. Thus, if this conjecture is false, it would make the following definition look highly suspect.
. This conjecture says that it makes sense to talk about whether or not a locally ordered ringed space looks locally like an order spectrum near a given point. Thus, if this conjecture is false, it would make the following definition look highly suspect.
Definition: An order scheme is a topological space ![]() equipped with a sheaf of ordered commutative rings
equipped with a sheaf of ordered commutative rings ![]() such that for some open cover of
such that for some open cover of ![]() , the restrictions of
, the restrictions of ![]() to the open sets in the cover are all isomorphic to order spectra of ordered commutative rings.
to the open sets in the cover are all isomorphic to order spectra of ordered commutative rings.
I don’t have any uses in mind for order schemes, but then again, I don’t know what ordinary schemes are for either and they are apparently useful, and order schemes seem like a natural analog of them.