Edit: Shortly after posting this, I found where the machinery I develop here was discussed in the literature. Real Algebraic Geometry by Bochnak, Coste, and Roy covers at least most of this material. I may eventually edit this to clean it up and adopt more standard notation, but don’t hold your breath.
Introduction
In algebraic geometry, an affine algebraic set is a subset of  which is the set of solutions to some finite set of polynomials. Since all ideals of
which is the set of solutions to some finite set of polynomials. Since all ideals of ![Rendered by QuickLaTeX.com \mathbb{C}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-3e5c4e262b36b4eee4ebf022f680a35e_l3.png) are finitely generated, this is equivalent to saying that an affine algebraic set is a subset of
are finitely generated, this is equivalent to saying that an affine algebraic set is a subset of  which is the set of solutions to some arbitrary set of polynomials.
which is the set of solutions to some arbitrary set of polynomials.
In semialgebraic geometry, a closed semialgebraic set is a subset of 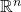 of the form
of the form 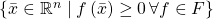 for some finite set of polynomials
for some finite set of polynomials ![Rendered by QuickLaTeX.com F\subseteq\mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-10bfef9fb8819d2b45fba627d6512f1e_l3.png) . Unlike in the case of affine algebraic sets, if
. Unlike in the case of affine algebraic sets, if ![Rendered by QuickLaTeX.com F\subseteq\mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-10bfef9fb8819d2b45fba627d6512f1e_l3.png) is an arbitrary set of polynomials,
is an arbitrary set of polynomials, 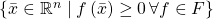 is not necessarily a closed semialgebraic set. As a result of this, the collection of closed semialgebraic sets are not the closed sets of a topology on
is not necessarily a closed semialgebraic set. As a result of this, the collection of closed semialgebraic sets are not the closed sets of a topology on 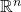 . In the topology on
. In the topology on 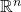 generated by closed semialgebraic sets being closed, the closed sets are the sets of the form
generated by closed semialgebraic sets being closed, the closed sets are the sets of the form 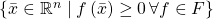 for arbitrary
for arbitrary ![Rendered by QuickLaTeX.com F\subseteq\mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-10bfef9fb8819d2b45fba627d6512f1e_l3.png) . Semialgebraic geometry usually restricts itself to the study of semialgebraic sets, but here I wish to consider all the closed sets of this topology. Notice that closed semialgebraic sets are also closed in the standard topology, so the standard topology is a refinement of this one. Notice also that the open ball
. Semialgebraic geometry usually restricts itself to the study of semialgebraic sets, but here I wish to consider all the closed sets of this topology. Notice that closed semialgebraic sets are also closed in the standard topology, so the standard topology is a refinement of this one. Notice also that the open ball 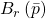 of radius
of radius  centered at
centered at 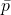 is the complement of the closed semialgebraic set
is the complement of the closed semialgebraic set 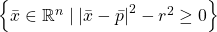 , and these open balls are a basis for the standard topology, so this topology is a refinement of the standard one. Thus, the topology I have defined is exactly the standard topology on
, and these open balls are a basis for the standard topology, so this topology is a refinement of the standard one. Thus, the topology I have defined is exactly the standard topology on 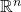 .
.
In algebra, instead of referring to a set of polynomials, it is often nicer to talk about the ideal generated by that set instead. What is the analog of an ideal in ordered algebra? It’s this thing:
Definition: If 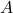 is a partially ordered commutative ring, a cone
is a partially ordered commutative ring, a cone 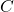 in
in 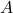 is a subsemiring of
is a subsemiring of 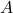 which contains all positive elements, and such that
which contains all positive elements, and such that 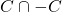 is an ideal of
is an ideal of 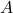 . By “subsemiring”, I mean a subset that contains
. By “subsemiring”, I mean a subset that contains 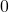 and
and 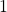 , and is closed under addition and multiplication (but not necessarily negation). If
, and is closed under addition and multiplication (but not necessarily negation). If 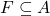 , the cone generated by
, the cone generated by 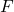 , denoted
, denoted 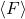 , is the smallest cone containing
, is the smallest cone containing 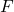 . Given a cone
. Given a cone 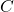 , the ideal
, the ideal 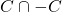 will be called the interior ideal of
will be called the interior ideal of 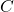 , and denoted
, and denoted 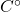 .
.
![Rendered by QuickLaTeX.com \mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-48307116e1f95cc6d56108104c40763d_l3.png) is partially ordered by
is partially ordered by 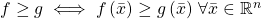 . If
. If ![Rendered by QuickLaTeX.com F\subseteq\mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-10bfef9fb8819d2b45fba627d6512f1e_l3.png) is a set of polynomials and
is a set of polynomials and 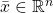 , then
, then  . Thus I can consider closed sets to be defined by cones. We now have a Galois connection between cones of
. Thus I can consider closed sets to be defined by cones. We now have a Galois connection between cones of ![Rendered by QuickLaTeX.com \mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-48307116e1f95cc6d56108104c40763d_l3.png) and subsets of
and subsets of 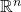 , given by, for a cone
, given by, for a cone 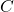 , its positive-set is
, its positive-set is 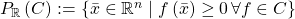 (I’m calling it the “positive-set” even though it is where the polynomials are all non-negative, because “non-negative-set” is kind of a mouthful), and for
(I’m calling it the “positive-set” even though it is where the polynomials are all non-negative, because “non-negative-set” is kind of a mouthful), and for 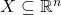 , its cone is
, its cone is ![Rendered by QuickLaTeX.com C_{\mathbb{R}}\left(X\right):=\left\{ f\in\mathbb{R}\left[x_{1},...,x_{n}\right]\mid f\left(\bar{x}\right)\geq0\,\forall\bar{x}\in X\right\}](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-0128abb72bca7764465ea7b34e267e27_l3.png) .
. 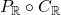 is closure in the standard topology on
is closure in the standard topology on 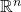 (the analog in algebraic geometry is closure in the Zariski topology on
(the analog in algebraic geometry is closure in the Zariski topology on  ). A closed set
). A closed set 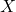 is semialgebraic if and only if it is the positive-set of a finitely-generated cone.
is semialgebraic if and only if it is the positive-set of a finitely-generated cone.
Quotients by cones, and coordinate rings
An affine algebraic set 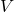 is associated with its coordinate ring
is associated with its coordinate ring ![Rendered by QuickLaTeX.com \mathbb{C}\left[V\right]:=\mathbb{C}\left[x_{1},...,x_{n}\right]/I\left(V\right)](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-b9dfb1d13ac247aaf617f52215fb4e0d_l3.png) . We can do something analogous for closed subsets of
. We can do something analogous for closed subsets of 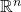 .
.
Definition: If 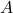 is a partially ordered commutative ring and
is a partially ordered commutative ring and 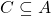 is a cone,
is a cone, 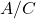 is the ring
is the ring 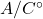 , equipped with the partial order given by
, equipped with the partial order given by 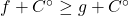 if and only if
if and only if 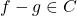 , for
, for 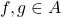 .
.
Definition: If 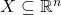 is closed, the coordinate ring of
is closed, the coordinate ring of 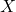 is
is ![Rendered by QuickLaTeX.com \mathbb{R}\left[X\right]:=\mathbb{R}\left[x_{1},...,x_{n}\right]/C\left(X\right)](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-a79e8be4eb8ba1ace7814b09755131cc_l3.png) . This is the ring of functions
. This is the ring of functions 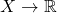 that are restrictions of polynomials, ordered by
that are restrictions of polynomials, ordered by 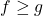 if and only if
if and only if 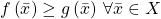 . For arbitrary
. For arbitrary 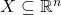 , the ring of regular functions on
, the ring of regular functions on 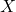 , denoted
, denoted 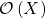 , consists of functions on
, consists of functions on 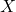 that are locally ratios of polynomials, again ordered by
that are locally ratios of polynomials, again ordered by 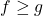 if and only if
if and only if 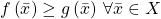 . Assigning its ring of regular functions to each open subset of
. Assigning its ring of regular functions to each open subset of 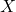 endows
endows 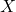 with a sheaf of partially ordered commutative rings.
with a sheaf of partially ordered commutative rings.
For closed 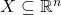 ,
, ![Rendered by QuickLaTeX.com \mathbb{R}\left[X\right]\subseteq\mathcal{O}\left(X\right)](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-781c3e027234e3b928a2deba14b0026c_l3.png) , and this inclusion is generally proper, both because it is possible to divide by polynomials that do not have roots in
, and this inclusion is generally proper, both because it is possible to divide by polynomials that do not have roots in 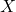 , and because
, and because 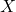 may be disconnected, making it possible to have functions given by different polynomials on different connected components.
may be disconnected, making it possible to have functions given by different polynomials on different connected components.
Positivstellensätze
What is 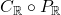 ? The Nullstellensatz says that its analog in algebraic geometry is the radical of an ideal. As such, we could say that the radical of a cone
? The Nullstellensatz says that its analog in algebraic geometry is the radical of an ideal. As such, we could say that the radical of a cone 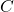 , denoted
, denoted 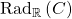 , is
, is 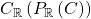 , and that a cone
, and that a cone 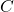 is radical if
is radical if 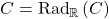 . In algebraic geometry, the Nullstellensatz shows that a notion of radical ideal defined without reference to algebraic sets in fact characterizes the ideals which are closed in the corresponding Galois connection. It would be nice to have a description of the radical of a cone that does not refer to the Galois connection. There is a semialgebraic analog of the Nullstellensatz, but it does not quite characterize radical cones.
. In algebraic geometry, the Nullstellensatz shows that a notion of radical ideal defined without reference to algebraic sets in fact characterizes the ideals which are closed in the corresponding Galois connection. It would be nice to have a description of the radical of a cone that does not refer to the Galois connection. There is a semialgebraic analog of the Nullstellensatz, but it does not quite characterize radical cones.
Positivstellensatz 1: If ![Rendered by QuickLaTeX.com C\subseteq\mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-7e075afa444ff7d4663ffdbc0914a289_l3.png) is a finitely-generated cone and
is a finitely-generated cone and ![Rendered by QuickLaTeX.com p\in\mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-c7294039116cfef61889f506f7ef55ee_l3.png) is a polynomial, then
is a polynomial, then 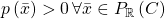 if and only if
if and only if 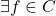 such that
such that 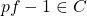 .
.
There are two ways in which this is unsatisfactory: first, it applies only to finitely-generated cones, and second, it tells us exactly which polynomials are strictly positive everywhere on a closed semialgebraic set, whereas we want to know which polynomials are non-negative everywhere on a set.
The second problem is easier to handle: a polynomial 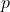 is non-negative everywhere on a set
is non-negative everywhere on a set 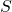 if and only if there is a decreasing sequence of polynomials
if and only if there is a decreasing sequence of polynomials 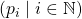 converging to
converging to 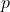 such that each
such that each 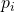 is strictly positive everywhere on
is strictly positive everywhere on 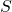 . Thus, to find
. Thus, to find 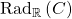 , it is enough to first find all the polynomials that are strictly positive everywhere on
, it is enough to first find all the polynomials that are strictly positive everywhere on 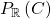 , and then take the closure under lower limits. Thus we have a characterization of radicals of finitely-generated cones.
, and then take the closure under lower limits. Thus we have a characterization of radicals of finitely-generated cones.
Positivstellensatz 2: If ![Rendered by QuickLaTeX.com C\subseteq\mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-7e075afa444ff7d4663ffdbc0914a289_l3.png) is a finitely-generated cone,
is a finitely-generated cone, 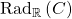 is the closure of
is the closure of ![Rendered by QuickLaTeX.com \left\{ p\in\mathbb{R}\left[x_{1},...,x_{n}\right]\mid\exists f\in C\, pf-1\in C\right\}](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-1d21527b01878943c62d0c0b3967098d_l3.png) , where the closure of a subset
, where the closure of a subset ![Rendered by QuickLaTeX.com X\subseteq\mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-a85be2ee182748a06b8e353f359fc0f4_l3.png) is defined to be the set of all polynomials in
is defined to be the set of all polynomials in ![Rendered by QuickLaTeX.com \mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-48307116e1f95cc6d56108104c40763d_l3.png) which are infima of chains contained in
which are infima of chains contained in 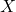 .
.
This still doesn’t even tell us what’s going on for cones which are not finitely-generated. However, we can generalize the Positivstellensatz to some other cones.
Positivstellensatz 3: Let ![Rendered by QuickLaTeX.com C\subseteq\mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-7e075afa444ff7d4663ffdbc0914a289_l3.png) be a cone containing a finitely-generated subcone
be a cone containing a finitely-generated subcone 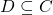 such that
such that 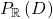 is compact. If
is compact. If ![Rendered by QuickLaTeX.com p\in\mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-c7294039116cfef61889f506f7ef55ee_l3.png) is a polynomial, then
is a polynomial, then 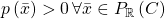 if and only if
if and only if 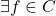 such that
such that 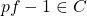 . As before, it follows that
. As before, it follows that 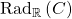 is the closure of
is the closure of ![Rendered by QuickLaTeX.com \left\{ p\in\mathbb{R}\left[x_{1},...,x_{n}\right]\mid\exists f\in C\, pf-1\in C\right\}](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-1d21527b01878943c62d0c0b3967098d_l3.png) .
.
proof: For a given ![Rendered by QuickLaTeX.com p\in\mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-c7294039116cfef61889f506f7ef55ee_l3.png) ,
, 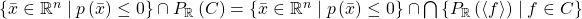 , an intersection of closed sets contained in the compact set
, an intersection of closed sets contained in the compact set 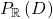 , which is thus empty if and only if some finite subcollection of them has empty intersection within
, which is thus empty if and only if some finite subcollection of them has empty intersection within 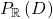 . Thus if
. Thus if 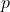 is strictly positive everywhere on
is strictly positive everywhere on 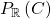 , then there is some finitely generated subcone
, then there is some finitely generated subcone 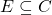 such that
such that 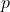 is strictly positive everywhere on
is strictly positive everywhere on 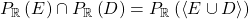 , and
, and 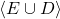 is finitely-generated, so by Positivstellensatz 1, there is
is finitely-generated, so by Positivstellensatz 1, there is 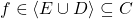 such that
such that 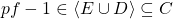 .
. 
For cones that are not finitely-generated and do not contain any finitely-generated subcones with compact positive-sets, the Positivstellensatz will usually fail. Thus, it seems likely that if there is a satisfactory general definition of radical for cones in arbitrary partially ordered commutative rings that agrees with this one in ![Rendered by QuickLaTeX.com \mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-48307116e1f95cc6d56108104c40763d_l3.png) , then there is also an abstract notion of “having a compact positive-set” for such cones, even though they don’t even have positive-sets associated with them.
, then there is also an abstract notion of “having a compact positive-set” for such cones, even though they don’t even have positive-sets associated with them.
Beyond 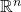
An example of cone for which the Positivstellensatz fails is ![Rendered by QuickLaTeX.com C_{\infty}:=\left\{ f\in\mathbb{R}\left[x\right]\mid\exists x\in\mathbb{R}\,\forall y\geq x\, f\left(y\right)\geq0\right\}](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-a1019b32499d4c437d7439d03ec4cfe8_l3.png) , the cone of polynomials that are non-negative on sufficiently large inputs (equivalently, the cone of polynomials that are either
, the cone of polynomials that are non-negative on sufficiently large inputs (equivalently, the cone of polynomials that are either 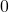 or have positive leading coefficient).
or have positive leading coefficient). 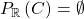 , and
, and 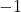 is strictly positive on
is strictly positive on 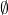 , but for
, but for 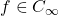 ,
, 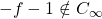 .
.
However, it doesn’t really look 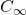 is trying to point to the empty set; instead,
is trying to point to the empty set; instead, 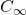 is trying to describe the set of all infinitely large reals, which only looks like the empty set because there are no infinitely large reals. Similar phenomena can occur even for cones that do contain finitely-generated subcones with compact positive-sets. For example, let
is trying to describe the set of all infinitely large reals, which only looks like the empty set because there are no infinitely large reals. Similar phenomena can occur even for cones that do contain finitely-generated subcones with compact positive-sets. For example, let ![Rendered by QuickLaTeX.com C_{\varepsilon}:=\left\{ f\in\mathbb{R}\left[x\right]\mid\exists x>0\,\forall y\in\left[0,x\right]\, f\left(y\right)\geq0\right\}](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-8f7e35c7181d51cd1e5181001eee769e_l3.png) .
. 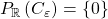 , but
, but 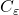 is trying to point out the set containing
is trying to point out the set containing 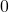 and all positive infinitesimals. Since
and all positive infinitesimals. Since 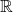 has no infinitesimals, this looks like
has no infinitesimals, this looks like 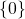 .
.
To formalize this intuition, we can change the Galois connection. We could say that for a cone ![Rendered by QuickLaTeX.com C\subseteq\mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-7e075afa444ff7d4663ffdbc0914a289_l3.png) ,
, 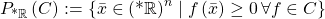 , where
, where 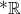 is the field of hyperreals. All you really need to know about
is the field of hyperreals. All you really need to know about 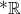 is that it is a big ordered field extension of
is that it is a big ordered field extension of 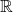 .
. 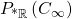 is the set of hyperreals that are bigger than any real number, and
is the set of hyperreals that are bigger than any real number, and 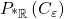 is the set of hyperreals that are non-negative and smaller than any positive real. The cone of a subset
is the set of hyperreals that are non-negative and smaller than any positive real. The cone of a subset 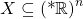 , denoted
, denoted 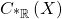 will be defined as before, still consisting only of polynomials with real coefficients. This defines a topology on
will be defined as before, still consisting only of polynomials with real coefficients. This defines a topology on 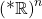 by saying that the closed sets are the fixed points of
by saying that the closed sets are the fixed points of 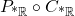 . This topology is not
. This topology is not 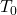 because, for example, there are many hyperreals that are larger than all reals, and they cannot be distinguished by polynomials with real coefficients. There is no use keeping track of the difference between points that are in the same closed sets. If you have a topology that is not
because, for example, there are many hyperreals that are larger than all reals, and they cannot be distinguished by polynomials with real coefficients. There is no use keeping track of the difference between points that are in the same closed sets. If you have a topology that is not 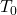 , you can make it
, you can make it 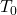 by identifying any pair of points that have the same closure. If we do this to
by identifying any pair of points that have the same closure. If we do this to 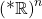 , we get what I’m calling ordered affine
, we get what I’m calling ordered affine 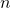 -space over
-space over 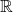 .
.
Definition: An 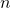 -type over
-type over 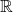 is a set
is a set 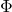 of inequalities, consisting of, for each polynomial
of inequalities, consisting of, for each polynomial ![Rendered by QuickLaTeX.com f\in\mathbb{R}\left[x_{1},..,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-d7185613ef1b22b100085a59c31e5fa6_l3.png) , one of the inequalities
, one of the inequalities 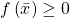 or
or 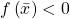 , such that there is some totally ordered field extension
, such that there is some totally ordered field extension 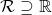 and
and 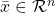 such that all inequalities in
such that all inequalities in 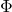 are true about
are true about 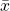 .
. 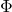 is called the type of
is called the type of 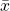 . Ordered affine
. Ordered affine 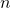 -space over
-space over 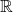 , denoted
, denoted  is the set of
is the set of 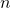 -types over
-types over 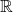 .
.
Compactness Theorem: Let 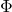 be a set of inequalities consisting of, for each polynomial
be a set of inequalities consisting of, for each polynomial ![Rendered by QuickLaTeX.com f\in\mathbb{R}\left[x_{1},..,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-d7185613ef1b22b100085a59c31e5fa6_l3.png) , one of the inequalities
, one of the inequalities 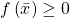 or
or 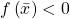 . Then
. Then 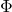 is an
is an 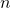 -type if and only if for any finite subset
-type if and only if for any finite subset 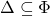 , there is
, there is 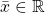 such that all inequalities in
such that all inequalities in  are true about
are true about 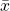 .
.
proof: Follows from the compactness theorem of first-order logic and the fact that ordered field extensions of 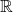 embed into elementary extensions of
embed into elementary extensions of 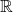 . The theorem is not obvious if you do not know what those mean.
. The theorem is not obvious if you do not know what those mean. 
An 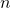 -type represents an
-type represents an 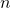 -tuple of elements of an ordered field extension of
-tuple of elements of an ordered field extension of 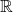 , up to the equivalence relation that identifies two such tuples that relate to
, up to the equivalence relation that identifies two such tuples that relate to 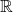 by polynomials in the same way. One way that a tuple of elements of an extension of
by polynomials in the same way. One way that a tuple of elements of an extension of 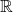 can relate to elements of
can relate to elements of 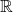 is to equal a tuple of elements of
is to equal a tuple of elements of 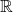 , so there is a natural inclusion
, so there is a natural inclusion 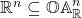 that associates an
that associates an 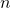 -tuple of reals with the set of polynomial inequalities that are true at that
-tuple of reals with the set of polynomial inequalities that are true at that 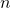 -tuple.
-tuple.
A tuple of polynomials ![Rendered by QuickLaTeX.com \left(f_{1},...,f_{m}\right)\in\left(\mathbb{R}\left[x_{1},...,x_{n}\right]\right)^{m}](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-cf103a55f6dd5ac9a0ef2a4c627c0431_l3.png) describes a function
describes a function 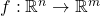 , which extends naturally to a function
, which extends naturally to a function 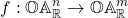 by
by 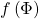 is the type of
is the type of 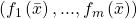 , where
, where 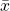 is an
is an 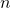 -tuple of elements of type
-tuple of elements of type 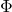 in an extension of
in an extension of 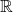 . In particular, a polynomial
. In particular, a polynomial ![Rendered by QuickLaTeX.com f\in\mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-babb8dabe8cbfbc58eaf430b52263e55_l3.png) extends to a function
extends to a function 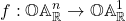 , and
, and 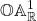 is totally ordered by
is totally ordered by 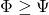 if and only if
if and only if 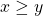 , where
, where 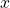 and
and 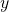 are elements of type
are elements of type 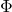 and
and 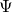 , respectively, in an extension of
, respectively, in an extension of 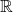 .
. 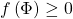 if and only if
if and only if 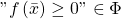 , so we can talk about inequalities satisfied by types in place of talking about inequalities contained in types.
, so we can talk about inequalities satisfied by types in place of talking about inequalities contained in types.
I will now change the Galois connection that we are talking about yet again (last time, I promise). It will now be a Galois connection between the set of cones in ![Rendered by QuickLaTeX.com \mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-48307116e1f95cc6d56108104c40763d_l3.png) and the set of subsets of
and the set of subsets of  . For a cone
. For a cone ![Rendered by QuickLaTeX.com C\subseteq\mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-7e075afa444ff7d4663ffdbc0914a289_l3.png) ,
, 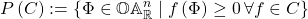 . For a set
. For a set 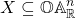 ,
, ![Rendered by QuickLaTeX.com C\left(X\right):=\left\{ f\in\mathbb{R}\left[x_{1},...,x_{n}\right]\mid f\left(\Phi\right)\geq0\,\forall\Phi\in X\right\}](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-610578a381ad7896d95b5e0dfdec9a2b_l3.png) . Again, this defines a topology on
. Again, this defines a topology on  by saying that fixed points of
by saying that fixed points of 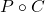 are closed.
are closed.  is
is 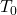 ; in fact, it is the
; in fact, it is the 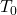 topological space obtained from
topological space obtained from 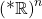 by identifying points with the same closure as mentioned earlier.
by identifying points with the same closure as mentioned earlier.  is also compact, as can be seen from the compactness theorem.
is also compact, as can be seen from the compactness theorem.  is not
is not 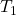 (unless
(unless 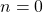 ). Note that model theorists have their own topology on
). Note that model theorists have their own topology on  , which is distinct from the one I use here, and is a refinement of it.
, which is distinct from the one I use here, and is a refinement of it.
The new Galois connection is compatible with the old one via the inclusion 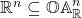 , in the sense that if
, in the sense that if 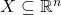 , then
, then 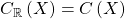 (where we identify
(where we identify 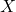 with its image in
with its image in  ), and for a cone
), and for a cone ![Rendered by QuickLaTeX.com C\subseteq\mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-7e075afa444ff7d4663ffdbc0914a289_l3.png) ,
, 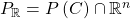 .
.
Like our intermediate Galois connection 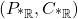 , our final Galois connection
, our final Galois connection 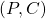 succeeds in distinguishing
succeeds in distinguishing 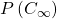 and
and 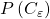 from
from 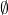 and
and 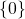 , respectively, in the desirable manner.
, respectively, in the desirable manner. 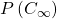 consists of the type of numbers larger than any real, and
consists of the type of numbers larger than any real, and 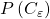 consists of the types of
consists of the types of 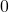 and of positive numbers smaller than any positive real.
and of positive numbers smaller than any positive real.
Just like for subsets of 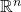 , a closed subset
, a closed subset 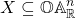 has a coordinate ring
has a coordinate ring ![Rendered by QuickLaTeX.com \mathbb{R}\left[X\right]:=\mathbb{R}\left[x_{1},...,x_{n}\right]/C\left(X\right)](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-a79e8be4eb8ba1ace7814b09755131cc_l3.png) , and an arbitrary
, and an arbitrary 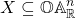 has a ring of regular functions
has a ring of regular functions 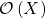 consisting of functions on
consisting of functions on 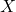 that are locally ratios of polynomials, ordered by
that are locally ratios of polynomials, ordered by 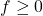 if and only if
if and only if  , where
, where 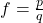 is a representation of
is a representation of 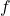 as a ratio of polynomials in a neighborhood of
as a ratio of polynomials in a neighborhood of 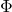 , either
, either 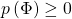 and
and 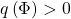 , or
, or 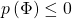 and
and 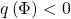 , and
, and 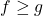 if and only if
if and only if 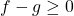 . As before,
. As before, ![Rendered by QuickLaTeX.com \mathbb{R}\left[X\right]\subseteq\mathcal{O}\left(X\right)](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-781c3e027234e3b928a2deba14b0026c_l3.png) for closed
for closed 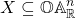 .
.
 is analogous to
is analogous to 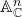 from algebraic geometry because if, in the above definitions, you replace “
from algebraic geometry because if, in the above definitions, you replace “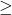 ” and “
” and “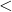 ” with “
” with “ ” and “
” and “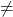 “, replace totally ordered field extensions with field extensions, and replace cones with ideals, then you recover a description of
“, replace totally ordered field extensions with field extensions, and replace cones with ideals, then you recover a description of 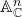 , in the sense of
, in the sense of ![Rendered by QuickLaTeX.com \text{Spec}\left(\mathbb{C}\left[x_{1},...,x_{n}\right]\right)](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-5a9cb4fecb3d4c40ef65d1f1fb9300b6_l3.png) .
.
What about an analog of projective space? Since we’re paying attention to order, we should look at spheres, not real projective space. The 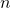 -sphere over
-sphere over 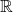 , denoted
, denoted 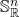 , can be described as the locus of
, can be described as the locus of 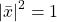 in
in  .
.
For any totally ordered field 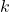 , we can define
, we can define 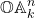 similarly to
similarly to  , as the space of
, as the space of 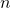 -types over
-types over 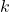 , defined as above, replacing
, defined as above, replacing 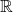 with
with 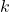 (although a model theorist would no longer call it the space of
(although a model theorist would no longer call it the space of 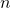 -types over
-types over 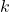 ). The compactness theorem is not true for arbitrary
). The compactness theorem is not true for arbitrary 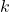 , but its corollary that
, but its corollary that 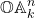 is compact still is true.
is compact still is true.
Visualizing  and
and 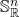
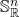 should be thought of as the
should be thought of as the 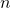 -sphere with infinitesimals in all directions around each point. Specifically,
-sphere with infinitesimals in all directions around each point. Specifically, 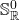 is just
is just 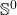 , a pair of points. The closed points of
, a pair of points. The closed points of 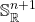 are the points of
are the points of 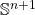 , and for each closed point
, and for each closed point 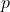 , there is an
, there is an 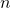 -sphere of infinitesimals around
-sphere of infinitesimals around 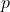 , meaning a copy of
, meaning a copy of 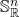 , each point of which has
, each point of which has 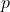 in its closure.
in its closure.
 should be thought of as
should be thought of as 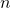 -space with infinitesimals in all directions around each point, and infinities in all directions. Specifically,
-space with infinitesimals in all directions around each point, and infinities in all directions. Specifically,  contains
contains 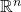 , and for each point
, and for each point 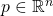 , there is an
, there is an  -sphere of infinitesimals around
-sphere of infinitesimals around 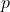 , and there is also a copy of
, and there is also a copy of 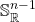 around the whole thing, the closed points of which are limits of rays in
around the whole thing, the closed points of which are limits of rays in 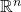 .
.
 and
and 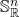 relate to each other the same way that
relate to each other the same way that 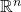 and
and 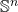 do. If you remove a closed point from
do. If you remove a closed point from 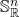 , you get
, you get  , where the sphere of infinitesimals around the removed closed point becomes the sphere of infinities of
, where the sphere of infinitesimals around the removed closed point becomes the sphere of infinities of  .
.
More generally, if 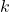 is a totally ordered field, let
is a totally ordered field, let 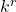 be its real closure.
be its real closure. 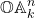 consists of the Cauchy completion of
consists of the Cauchy completion of 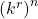 (as a metric space with distances valued in
(as a metric space with distances valued in 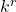 ), and for each point
), and for each point 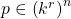 (though not for points that are limits of Cauchy sequences that do not converge in
(though not for points that are limits of Cauchy sequences that do not converge in 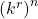 ), an
), an  -sphere
-sphere 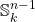 of infinitesimals around
of infinitesimals around 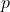 , and an
, and an  -sphere
-sphere 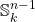 around the whole thing, where
around the whole thing, where 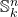 is the locus of
is the locus of 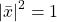 in
in 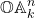 .
. 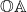 does not distinguish between fields with the same real closure.
does not distinguish between fields with the same real closure.
More Positivstellensätze
This Galois connection gives us a new notion of what it means for a cone to be radical, which is distinct from the old one and is better, so I will define 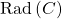 to be
to be 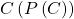 . A cone
. A cone 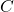 will be called radical if
will be called radical if 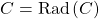 . Again, it would be nice to be able to characterize radical cones without referring to the Galois connection. And this time, I can do it. Note that since
. Again, it would be nice to be able to characterize radical cones without referring to the Galois connection. And this time, I can do it. Note that since  is compact, the proof of Positivstellensatz 3 shows that in our new context, the Positivstellensatz holds for all cones, since even the subcone generated by
is compact, the proof of Positivstellensatz 3 shows that in our new context, the Positivstellensatz holds for all cones, since even the subcone generated by 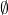 has a compact positive-set.
has a compact positive-set.
Positivstellensatz 4: If ![Rendered by QuickLaTeX.com C\subseteq\mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-7e075afa444ff7d4663ffdbc0914a289_l3.png) is a cone and
is a cone and ![Rendered by QuickLaTeX.com p\in\mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-c7294039116cfef61889f506f7ef55ee_l3.png) is a polynomial, then
is a polynomial, then 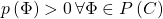 if and only if
if and only if 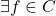 such that
such that 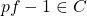 .
.
However, we can no longer add in lower limits of sequences of polynomials. For example, 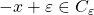 for all real
for all real 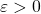 , but
, but 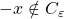 , even though
, even though 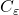 is radical. This happens because, where
is radical. This happens because, where 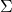 is the type of positive infinitesimals,
is the type of positive infinitesimals, 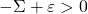 for real
for real 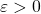 , but
, but 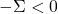 . However, we can add in lower limits of sequences contained in finitely-generated subcones, and this is all we need to add, so this characterizes radical cones.
. However, we can add in lower limits of sequences contained in finitely-generated subcones, and this is all we need to add, so this characterizes radical cones.
Positivstellensatz 5: If ![Rendered by QuickLaTeX.com C\subseteq\mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-7e075afa444ff7d4663ffdbc0914a289_l3.png) is a cone,
is a cone, 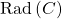 is the union over all finitely-generated subcones
is the union over all finitely-generated subcones 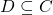 of the closure of
of the closure of ![Rendered by QuickLaTeX.com \left\{ p\in\mathbb{R}\left[x_{1},...,x_{n}\right]\mid\exists f\in D\, pf-1\in D\right\}](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-b44a257003d1663637480ff7cb35b22d_l3.png) (again the closure of a subset
(again the closure of a subset ![Rendered by QuickLaTeX.com X\subseteq\mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-a85be2ee182748a06b8e353f359fc0f4_l3.png) is defined to be the set of all polynomials in
is defined to be the set of all polynomials in ![Rendered by QuickLaTeX.com \mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-48307116e1f95cc6d56108104c40763d_l3.png) which are infima of chains contained in
which are infima of chains contained in 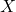 ).
).
Proof: Suppose 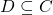 is a subcone generated by a finite set
is a subcone generated by a finite set 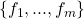 , and
, and 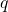 is the infimum of a chain
is the infimum of a chain ![Rendered by QuickLaTeX.com \left\{ q_{\alpha}\right\} _{\alpha\in A}\subseteq\left\{ p\in\mathbb{R}\left[x_{1},...,x_{n}\right]\mid\exists f\in D\, pf-1\in D\right\}](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-ab89f3733ac0c45c39667afd1e5906b7_l3.png) . For any
. For any 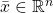 , if
, if 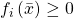 for each
for each 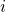 , then
, then 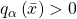 for each
for each 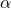 , and hence
, and hence 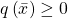 . That is, the finite set of inequalities
. That is, the finite set of inequalities 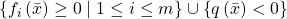 does not hold anywhere in
does not hold anywhere in 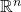 . By the compactness theorem, there are no
. By the compactness theorem, there are no 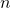 -types satisfying all those inequalities. Given
-types satisfying all those inequalities. Given 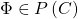 ,
, 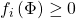 , so
, so 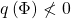 ; that is,
; that is, 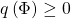 .
.
Conversely, suppose 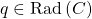 . Then by the compactness theorem, there are some
. Then by the compactness theorem, there are some 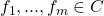 such that
such that 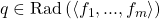 . Then
. Then 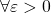 ,
, 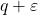 is strictly positive on
is strictly positive on 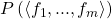 , and hence by Positivstellensatz 4,
, and hence by Positivstellensatz 4, 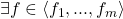 such that
such that 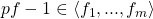 . That is,
. That is, 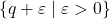 is a chain contained in
is a chain contained in 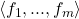 , a finitely-generated subcone of
, a finitely-generated subcone of 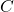 , whose infimum is
, whose infimum is 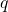 .
. 
Ordered commutative algebra
Even though they are technically not isomorphic,  and
and ![Rendered by QuickLaTeX.com \text{Spec}\left(\mathbb{C}\left[x_{1},...,x_{n}\right]\right)](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-5a9cb4fecb3d4c40ef65d1f1fb9300b6_l3.png) are closely related, and can often be used interchangeably. Of the two,
are closely related, and can often be used interchangeably. Of the two, ![Rendered by QuickLaTeX.com \text{Spec}\left(\mathbb{C}\left[x_{1},...,x_{n}\right]\right)](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-5a9cb4fecb3d4c40ef65d1f1fb9300b6_l3.png) is of a form that can be more easily generalized to more abstruse situations in algebraic geometry, which may indicate that it is the better thing to talk about, whereas
is of a form that can be more easily generalized to more abstruse situations in algebraic geometry, which may indicate that it is the better thing to talk about, whereas  is merely the simpler thing that is easier to think about and just as good in practice in many contexts. In contrast,
is merely the simpler thing that is easier to think about and just as good in practice in many contexts. In contrast, 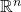 and
and  are different in important ways. The situation in algebraic geometry provides further reason to pay more attention to
are different in important ways. The situation in algebraic geometry provides further reason to pay more attention to  than to
than to 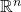 .
.
The next thing to look for would be an analog of the spectrum of a ring for a partially ordered commutative ring (I will henceforth abbreviate “partially ordered commutative ring” as “ordered ring” in order to cut down on the profusion of adjectives) in a way that makes use of the order, and gives us  when applied to
when applied to ![Rendered by QuickLaTeX.com \mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-48307116e1f95cc6d56108104c40763d_l3.png) . I will call it the order spectrum of an ordered ring
. I will call it the order spectrum of an ordered ring 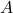 , denoted
, denoted 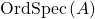 . Then of course
. Then of course 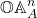 can be defined as
can be defined as ![Rendered by QuickLaTeX.com \text{OrdSpec}\left(A\left[x_{1},...,x_{n}\right]\right)](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-1e37b218fd9b68a3d848f161eef33f1b_l3.png) .
. 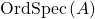 should be, of course, the set of prime cones. But what even is a prime cone?
should be, of course, the set of prime cones. But what even is a prime cone?
Definition: A cone 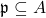 is prime if
is prime if 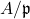 is a totally ordered integral domain.
is a totally ordered integral domain.
Definition: 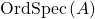 is the set of prime cones in
is the set of prime cones in 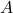 , equipped with the topology whose closed sets are the sets of prime cones containing a given cone.
, equipped with the topology whose closed sets are the sets of prime cones containing a given cone.
An 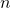 -type
-type 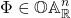 can be seen as a cone, by identifying it with
can be seen as a cone, by identifying it with ![Rendered by QuickLaTeX.com \left\{ f\in\mathbb{R}\left[x_{1},...,x_{n}\right]\mid f\left(\Phi\right)\geq0\right\}](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-29b64dd4a9e442027851a91860b9f377_l3.png) , aka
, aka 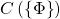 . Under this identification,
. Under this identification, ![Rendered by QuickLaTeX.com \mathbb{OA}_{\mathbb{R}}^{n}=\text{OrdSpec}\left(\mathbb{R}\left[x_{1},...,x_{n}\right]\right)](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-698cd8e1f2bac1092933cf46c7b62b93_l3.png) , as desired. The prime cones in
, as desired. The prime cones in ![Rendered by QuickLaTeX.com \mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-48307116e1f95cc6d56108104c40763d_l3.png) are also the radical cones
are also the radical cones 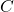 such that
such that 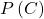 is irreducible. Notice that irreducible subsets of
is irreducible. Notice that irreducible subsets of  are much smaller than irreducible subsets of
are much smaller than irreducible subsets of 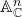 ; in particular, none of them contain more than one element of
; in particular, none of them contain more than one element of 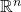 .
.
There is also a natural notion of maximal cone.
Definition: A cone 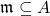 is maximal if
is maximal if 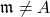 and there are no strictly intermediate cones between
and there are no strictly intermediate cones between 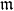 and
and 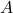 . Equivalently, if
. Equivalently, if 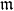 is prime and closed in
is prime and closed in 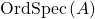 .
.
Maximal ideals of ![Rendered by QuickLaTeX.com \mathbb{C}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-3e5c4e262b36b4eee4ebf022f680a35e_l3.png) correspond to elements of
correspond to elements of  . And the cones of elements of
. And the cones of elements of 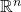 are maximal cones in
are maximal cones in ![Rendered by QuickLaTeX.com \mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-48307116e1f95cc6d56108104c40763d_l3.png) , but unlike in the complex case, these are not all the maximal cones, since there are closed points in
, but unlike in the complex case, these are not all the maximal cones, since there are closed points in  outside of
outside of 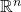 . For example,
. For example, 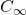 is a maximal cone, and the type of numbers greater than all reals is closed. To characterize the cones of elements of
is a maximal cone, and the type of numbers greater than all reals is closed. To characterize the cones of elements of 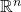 , we need something slightly different.
, we need something slightly different.
Definition: A cone 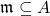 is ideally maximal if
is ideally maximal if 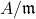 is a totally ordered field. Equivalently, if
is a totally ordered field. Equivalently, if 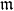 is maximal and
is maximal and 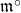 is a maximal ideal.
is a maximal ideal.
Elements of 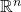 correspond to ideally maximal cones of
correspond to ideally maximal cones of ![Rendered by QuickLaTeX.com \mathbb{R}\left[x_{1},...,x_{n}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-48307116e1f95cc6d56108104c40763d_l3.png) .
.
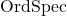 also allows us to define the radical of a cone in an arbitrary partially ordered commutative ring.
also allows us to define the radical of a cone in an arbitrary partially ordered commutative ring.
Definition: For a cone 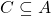 ,
, 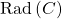 is the intersection of all prime cones containing
is the intersection of all prime cones containing 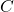 .
. 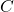 is radical if
is radical if 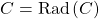 .
.
Conjecture: 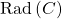 is the union over all finitely-generated subcones
is the union over all finitely-generated subcones 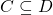 of the closure of
of the closure of 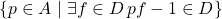 (as before, the closure of a subset
(as before, the closure of a subset 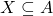 is defined to be the set of all elements of
is defined to be the set of all elements of 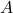 which are infima of chains contained in
which are infima of chains contained in 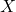 ).
).
Order schemes
Definition: An ordered ringed space is a topological space equipped with a sheaf of ordered rings. An ordered ring is local if it has a unique ideally maximal cone, and a locally ordered ringed space is an ordered ringed space whose stalks are local.
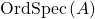 can be equipped with a sheaf of ordered rings
can be equipped with a sheaf of ordered rings 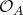 , making it a locally ordered ringed space.
, making it a locally ordered ringed space.
Definition: For a prime cone 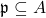 , the localization of
, the localization of 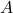 at
at 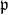 , denoted
, denoted 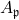 , is the ring
, is the ring 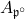 equipped with an ordering that makes it a local ordered ring. This will be the stalk at
equipped with an ordering that makes it a local ordered ring. This will be the stalk at 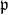 of
of 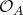 . A fraction
. A fraction 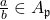 (
(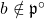 ) is also an element of
) is also an element of 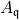 for any prime cone
for any prime cone 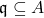 whose interior ideal does not contain
whose interior ideal does not contain 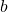 . This is an open neighborhood of
. This is an open neighborhood of 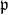 (its complement is the set of prime cones containing
(its complement is the set of prime cones containing 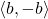 ). There is a natural map
). There is a natural map 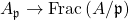 given by
given by 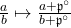 , and the total order on
, and the total order on 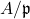 extends uniquely to a total order on the fraction field, so for
extends uniquely to a total order on the fraction field, so for 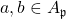 , we can say that
, we can say that 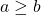 at
at 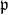 if this is true of their images in
if this is true of their images in 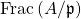 . We can then say that
. We can then say that 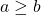 near
near 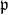 if
if 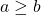 at every point in some neighborhood of
at every point in some neighborhood of 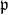 , which defines the ordering on
, which defines the ordering on 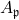 .
.
Definition: For open 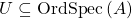 ,
, 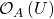 consists of elements of
consists of elements of 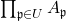 that are locally ratios of elements of
that are locally ratios of elements of 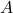 .
. 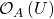 is ordered by
is ordered by 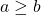 if and only if
if and only if 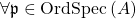
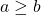 near
near 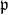 (equivalently, if
(equivalently, if 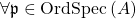
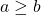 at
at 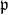 ).
).
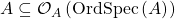 , and this inclusion can be proper. Conjecture:
, and this inclusion can be proper. Conjecture: 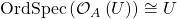 as locally ordered ringed spaces for open
as locally ordered ringed spaces for open 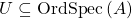 . This conjecture says that it makes sense to talk about whether or not a locally ordered ringed space looks locally like an order spectrum near a given point. Thus, if this conjecture is false, it would make the following definition look highly suspect.
. This conjecture says that it makes sense to talk about whether or not a locally ordered ringed space looks locally like an order spectrum near a given point. Thus, if this conjecture is false, it would make the following definition look highly suspect.
Definition: An order scheme is a topological space 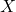 equipped with a sheaf of ordered commutative rings
equipped with a sheaf of ordered commutative rings 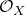 such that for some open cover of
such that for some open cover of 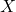 , the restrictions of
, the restrictions of 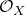 to the open sets in the cover are all isomorphic to order spectra of ordered commutative rings.
to the open sets in the cover are all isomorphic to order spectra of ordered commutative rings.
I don’t have any uses in mind for order schemes, but then again, I don’t know what ordinary schemes are for either and they are apparently useful, and order schemes seem like a natural analog of them.
![]() is said to be at least as large as a set
is said to be at least as large as a set ![]() if there is an injection from
if there is an injection from ![]() into
into ![]() , the same size as
, the same size as ![]() if there is a bijection between
if there is a bijection between ![]() and
and ![]() , and strictly larger than
, and strictly larger than ![]() if it is at least as large as
if it is at least as large as ![]() but not the same size. So all this result is saying is that if the axiom of choice is false, then there are two sets, neither of which can be injected into the other. It’s not hard to find two groups without an injective homomorphism between them in either direction, and not hard to find two topological spaces without any injective continuous maps between them in either direction. So why not sets?
but not the same size. So all this result is saying is that if the axiom of choice is false, then there are two sets, neither of which can be injected into the other. It’s not hard to find two groups without an injective homomorphism between them in either direction, and not hard to find two topological spaces without any injective continuous maps between them in either direction. So why not sets?![]() on a set
on a set ![]() such that there are strictly more equivalence classes of
such that there are strictly more equivalence classes of ![]() than there are elements of
than there are elements of ![]() . For instance, if all subsets of
. For instance, if all subsets of ![]() are Lebesgue measurable, then this can be done with an equivalence relation on
are Lebesgue measurable, then this can be done with an equivalence relation on ![]() , namely
, namely ![]() iff
iff ![]() .
.![]() to
to ![]() but no bijection between them. Instead, you can think about it as
but no bijection between them. Instead, you can think about it as ![]() and
and ![]() being flexible in the ways that allow
being flexible in the ways that allow ![]() to fit inside
to fit inside ![]() , but rigid in ways that prevent
, but rigid in ways that prevent ![]() from fitting inside
from fitting inside ![]() , rather than in terms of bigness.
, rather than in terms of bigness.![]() has strictly larger cardinality than
has strictly larger cardinality than ![]() ” sounds more absurd than “
” sounds more absurd than “![]() and
and ![]() have incomparable cardinalities” does, but it really shouldn’t, since these are almost the same thing. The reason these are almost the same is that an infinite set can be in bijection with the union of two disjoint copies of itself, another phenomenon that could be thought of as an absurdity if the identification of cardinality with size is taken too literally, but which you have probably long since gotten used to. If
have incomparable cardinalities” does, but it really shouldn’t, since these are almost the same thing. The reason these are almost the same is that an infinite set can be in bijection with the union of two disjoint copies of itself, another phenomenon that could be thought of as an absurdity if the identification of cardinality with size is taken too literally, but which you have probably long since gotten used to. If ![]() and
and ![]() have incomparable cardinalities and
have incomparable cardinalities and ![]() can be put into bijection with two copies of itself, then, using such a bijection to identify
can be put into bijection with two copies of itself, then, using such a bijection to identify ![]() with two copies of itself, mod out one of them by
with two copies of itself, mod out one of them by ![]() while leaving the other unchanged. The set of equivalence classes of this new equivalence relation looks like
while leaving the other unchanged. The set of equivalence classes of this new equivalence relation looks like ![]() , which
, which ![]() easily injects into.
easily injects into.![]() such that
such that ![]() can’t inject into
can’t inject into ![]() ; the only obvious reason
; the only obvious reason ![]() should be able to inject into
should be able to inject into ![]() is that you could pick an element of each equivalence class, but the possibility of doing this is a restatement of the axiom of choice. For instance, in the example of
is that you could pick an element of each equivalence class, but the possibility of doing this is a restatement of the axiom of choice. For instance, in the example of ![]() and
and ![]() , a set consisting of one element from each equivalence class would not be Lebesgue measurable, and thus doesn’t exist if all sets are Lebesgue measurable.
, a set consisting of one element from each equivalence class would not be Lebesgue measurable, and thus doesn’t exist if all sets are Lebesgue measurable.![]() , since everything is coded for by integers. But Cantor’s theorem is constructive, so it applies here. Given a computable sequence of computable reals, we can produce a computation of a real number that isn’t in the sequence. So the integers and the (computable) reals here have different “cardinalities” in the sense that, due to their differing computational structure, there’s no bijection between them in this computability universe.
, since everything is coded for by integers. But Cantor’s theorem is constructive, so it applies here. Given a computable sequence of computable reals, we can produce a computation of a real number that isn’t in the sequence. So the integers and the (computable) reals here have different “cardinalities” in the sense that, due to their differing computational structure, there’s no bijection between them in this computability universe.![]() , so how could something countable be a model of ZFC? The answer is that an infinite set being uncountable just means that there’s no bijection between it and
, so how could something countable be a model of ZFC? The answer is that an infinite set being uncountable just means that there’s no bijection between it and ![]() . A countable model of ZFC can contain a countable set but not contain any of the bijections between it and
. A countable model of ZFC can contain a countable set but not contain any of the bijections between it and ![]() ; then, internally to the model, this set qualifies as uncountable. This is sometimes described as the countable model of ZFC “believing” that some of its sets are uncountable, but being “wrong”. I think this is a little sloppy; models of ZFC are just mathematical structures, not talk radio hosts with bad opinions. Restricting attention to a certain model of ZFC means imposing additional structure on its elements; namely that structure which is preserved by the functions in the model. This additional structure isn’t respected by functions outside the model, just like equipping a set with a topology imposes structure on it that isn’t respected by discontinuous maps.
; then, internally to the model, this set qualifies as uncountable. This is sometimes described as the countable model of ZFC “believing” that some of its sets are uncountable, but being “wrong”. I think this is a little sloppy; models of ZFC are just mathematical structures, not talk radio hosts with bad opinions. Restricting attention to a certain model of ZFC means imposing additional structure on its elements; namely that structure which is preserved by the functions in the model. This additional structure isn’t respected by functions outside the model, just like equipping a set with a topology imposes structure on it that isn’t respected by discontinuous maps.![]() in practice, they often naturally carry separable topologies on them, so I think of
in practice, they often naturally carry separable topologies on them, so I think of ![]() as being thicker than
as being thicker than ![]() , but no longer. Since smaller ordinals are initial segments of larger ordinals, I think of
, but no longer. Since smaller ordinals are initial segments of larger ordinals, I think of ![]() , the cardinality of the first uncountable ordinal, as longer than
, the cardinality of the first uncountable ordinal, as longer than ![]() , but no thicker.
, but no thicker. ![]() being well-orderable would mean we can rearrange something thick into something long.
being well-orderable would mean we can rearrange something thick into something long.![]() ) out of something thick (
) out of something thick (![]() ) by modding out by an equivalence relation. (This gives another example of a quotient of
) by modding out by an equivalence relation. (This gives another example of a quotient of ![]() that, axiom of choice aside, it’s perfectly reasonable to think shouldn’t fit back inside
that, axiom of choice aside, it’s perfectly reasonable to think shouldn’t fit back inside ![]() ). This is because
). This is because ![]() is the cardinality of the set of countable ordinals, each countable ordinal is the order-type of a well-ordering of
is the cardinality of the set of countable ordinals, each countable ordinal is the order-type of a well-ordering of ![]() , and well-orderings on
, and well-orderings on ![]() are binary relations on
are binary relations on ![]() , aka subsets of
, aka subsets of ![]() . So, starting with
. So, starting with ![]() (with cardinality
(with cardinality ![]() ), say that any two elements that are both well-orderings of the same order-type are equivalent (and, if you want to end up with just
), say that any two elements that are both well-orderings of the same order-type are equivalent (and, if you want to end up with just ![]() , rather than
, rather than ![]() , also say that all the left-overs that aren’t well-orderings are equivalent to each other). The set of equivalence classes then corresponds to the set of countable ordinals (plus whatever you did with the leftovers that aren’t well-orderings).
, also say that all the left-overs that aren’t well-orderings are equivalent to each other). The set of equivalence classes then corresponds to the set of countable ordinals (plus whatever you did with the leftovers that aren’t well-orderings).![]() statements (a broad class of statements that arguably includes everything concrete or directly applicable in the real world) that can be proved in ZFC can also be proved in ZF, so assuming the axiom of choice isn’t going to lead us astray about concrete things regardless of whether it is true in some fundamental sense, but assuming the axiom of choice can sometimes make it easier to prove something even if in theory it could be proved otherwise. This seems like a good reason to assume the axiom of choice to me, but that’s different from the axiom of choice being fundamentally true, or things that can happen if the axiom of choice is false being absurd.
statements (a broad class of statements that arguably includes everything concrete or directly applicable in the real world) that can be proved in ZFC can also be proved in ZF, so assuming the axiom of choice isn’t going to lead us astray about concrete things regardless of whether it is true in some fundamental sense, but assuming the axiom of choice can sometimes make it easier to prove something even if in theory it could be proved otherwise. This seems like a good reason to assume the axiom of choice to me, but that’s different from the axiom of choice being fundamentally true, or things that can happen if the axiom of choice is false being absurd.![Rendered by QuickLaTeX.com \left\langle \left[\begin{array}{c} t_{1}\\ x_{1}\\ y_{1}\\ z_{1} \end{array}\right],\left[\begin{array}{c} t_{2}\\ x_{2}\\ y_{2}\\ z_{2} \end{array}\right]\right\rangle =-c^{2}t_{1}t_{2}+x_{1}x_{2}+y_{1}y_{2}+z_{1}z_{1}](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-3f69ac65dafced1956311fcc8ca7ad7d_l3.png) . As a map
. As a map ![Rendered by QuickLaTeX.com \left[\begin{array}{c} t\\ x\\ y\\ z \end{array}\right]\mapsto\left[\begin{array}{cccc} -c^{2}t & x & y & z\end{array}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-72e747f3cc3e89f291d8ec1e182e0411_l3.png) . The inverse map
. The inverse map ![Rendered by QuickLaTeX.com \left[\begin{array}{cccc} \tau & \alpha & \beta & \gamma\end{array}\right]\mapsto\left[\begin{array}{c} -c^{-2}\tau\\ \alpha\\ \beta\\ \gamma \end{array}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-ca3ccd11aae199844acb1b6fc086afce_l3.png) , or, as an inner product on
, or, as an inner product on ![Rendered by QuickLaTeX.com \left\langle \left[\begin{array}{c} t_{1}\\ x_{1}\\ y_{1}\\ z_{1} \end{array}\right],\left[\begin{array}{c} t_{2}\\ x_{2}\\ y_{2}\\ z_{2} \end{array}\right]\right\rangle =-t_{1}t_{2}+c^{-2}x_{1}x_{2}+c^{-2}y_{1}y_{2}+c^{-2}z_{1}z_{1}](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-af984de58ef446b9c213959ef4a85274_l3.png) , or, as a map
, or, as a map ![Rendered by QuickLaTeX.com \left[\begin{array}{c} t\\ x\\ y\\ z \end{array}\right]\mapsto\left[\begin{array}{cccc} -t & c^{-2}x & c^{-2}y & c^{-2}z\end{array}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-164bacb88351b209a71b5d0ae60f4eda_l3.png) . The limit
. The limit ![Rendered by QuickLaTeX.com \left\langle \left[\begin{array}{c} t_{1}\\ x_{1}\\ y_{1}\\ z_{1} \end{array}\right],\left[\begin{array}{c} t_{2}\\ x_{2}\\ y_{2}\\ z_{2} \end{array}\right]\right\rangle =-t_{1}t_{2}](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-7d81eb8a4fb8e8e88bad52901712cbb6_l3.png) , and our spatial inner product on the dual space
, and our spatial inner product on the dual space ![Rendered by QuickLaTeX.com \left[\begin{array}{c} t\\ x\\ y\\ z \end{array}\right]\mapsto\left[\begin{array}{cccc} -t & 0 & 0 & 0\end{array}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-98d00b56bab5ecb597bd27c98b56d60a_l3.png) and
and ![Rendered by QuickLaTeX.com \left[\begin{array}{cccc} \tau & \alpha & \beta & \gamma\end{array}\right]\mapsto\left[\begin{array}{c} 0\\ \alpha\\ \beta\\ \gamma \end{array}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-ee71dcb62c29bd1bdb33a867578c1746_l3.png) . (I did say that this should only work if we have to divide by
. (I did say that this should only work if we have to divide by