An ![]() -dimensional quadratic form over a field
-dimensional quadratic form over a field ![]() is a polynomial in
is a polynomial in ![]() variables with coefficients in
variables with coefficients in ![]() that is homogeneous of degree
that is homogeneous of degree ![]() . More abstractly, a quadratic form on a vector space
. More abstractly, a quadratic form on a vector space ![]() is a function
is a function ![]() that comes from a homogeneous degree-
that comes from a homogeneous degree-![]() polynomial in the linear functions on
polynomial in the linear functions on ![]() .
.
I’ll start off with some comments on why quadratic forms are a natural type of object to want to classify. Then I’ll review well-known classifications of the quadratic forms over ![]() and
and ![]() . Then I’ll give the classification of quadratic forms over finite fields of odd characteristic. Then I’ll go over some counting problems related to quadratic forms over finite fields, which might get tedious. Finally, and perhaps most interestingly, I’ll tell you how
. Then I’ll give the classification of quadratic forms over finite fields of odd characteristic. Then I’ll go over some counting problems related to quadratic forms over finite fields, which might get tedious. Finally, and perhaps most interestingly, I’ll tell you how ![]() and
and ![]() are secretly related to finite fields, and what this means for quadratic forms over each of them.
are secretly related to finite fields, and what this means for quadratic forms over each of them.
I’ll actually just focus on nondegenerate quadratic forms. A quadratic form ![]() is degenerate if there is a nonzero vector
is degenerate if there is a nonzero vector ![]() that is “
that is “![]() -orthogonal” to every vector, meaning that
-orthogonal” to every vector, meaning that ![]() for every vector
for every vector ![]() . In this case, we can change coordinates so that
. In this case, we can change coordinates so that ![]() is a standard basis vector, and in these coordinates,
is a standard basis vector, and in these coordinates, ![]() doesn’t use one of the variables, so the same polynomial gives us an
doesn’t use one of the variables, so the same polynomial gives us an ![]() -dimensional quadratic form. We can iterate this until we get a nondegenerate quadratic form, so
-dimensional quadratic form. We can iterate this until we get a nondegenerate quadratic form, so ![]() -dimensional quadratic forms are in some sense equivalent to at-most-
-dimensional quadratic forms are in some sense equivalent to at-most-![]() -dimensional nondegenerate quadratic forms (in terms of abstract vector spaces, a quadratic form on a vector space is a nondegenerate quadratic form on some quotient of it). Because of this, the interesting parts of understanding quadratic forms is mostly just understanding the nondegenerate quadratic forms.
-dimensional nondegenerate quadratic forms (in terms of abstract vector spaces, a quadratic form on a vector space is a nondegenerate quadratic form on some quotient of it). Because of this, the interesting parts of understanding quadratic forms is mostly just understanding the nondegenerate quadratic forms.
An important tool will be the fact that quadratic forms are essentially the same thing as symmetric bilinear forms. An ![]() -dimensional symmetric bilinear form over a field
-dimensional symmetric bilinear form over a field ![]() is a function
is a function ![]() that is symmetric (i.e.
that is symmetric (i.e. ![]() ), and linear in each component (i.e., for any
), and linear in each component (i.e., for any ![]() , the function
, the function ![]() is linear). From any symmetric bilinear form
is linear). From any symmetric bilinear form ![]() , we can get a quadratic form
, we can get a quadratic form ![]() by
by ![]() , and from any quadratic form
, and from any quadratic form ![]() , that symmetric bilinear form can be recovered by
, that symmetric bilinear form can be recovered by ![]() . This means that there’s a natural bijection between quadratic forms and symmetric bilinear forms, so I could have just as easily said this was a post about symmetric bilinear forms over finite fields (of characteristic other than
. This means that there’s a natural bijection between quadratic forms and symmetric bilinear forms, so I could have just as easily said this was a post about symmetric bilinear forms over finite fields (of characteristic other than ![]() ). Throughout this post, whenever
). Throughout this post, whenever ![]() denotes some quadratic form, I’ll use
denotes some quadratic form, I’ll use ![]() to denote the corresponding symmetric bilinear form. Of course, this bijection involves dividing by
to denote the corresponding symmetric bilinear form. Of course, this bijection involves dividing by ![]() , so it does not work in characteristic
, so it does not work in characteristic ![]() , and this is related to why the situation is much more complicated over fields of characteristic
, and this is related to why the situation is much more complicated over fields of characteristic ![]() .
.
In coordinates, quadratic forms and symmetric bilinear forms can both represented by symmetric matrices. A symmetric matrix ![]() represents the quadratic form
represents the quadratic form ![]() , and the corresponding symmetric bilinear form
, and the corresponding symmetric bilinear form ![]() . From the symmetric bilinear form, you can extract the matrix representing it:
. From the symmetric bilinear form, you can extract the matrix representing it: ![]() , where
, where ![]() are the standard basis vectors.
are the standard basis vectors.
Two quadratic forms are equivalent if you can turn one into the other with an invertible linear transformation. That is, ![]() and
and ![]() are equivalent if there’s an invertible linear transformation
are equivalent if there’s an invertible linear transformation ![]() such that
such that ![]() for every vector
for every vector ![]() . In coordinates, quadratic forms represented by matrices
. In coordinates, quadratic forms represented by matrices ![]() and
and ![]() are equivalent if there’s an invertible matrix
are equivalent if there’s an invertible matrix ![]() such that
such that ![]() . When I said earlier that I would classify the quadratic forms over
. When I said earlier that I would classify the quadratic forms over ![]() ,
, ![]() , and finite fields of odd characteristic, what I meant is classify nondegenerate quadratic forms up to this notion of equivalence.
, and finite fields of odd characteristic, what I meant is classify nondegenerate quadratic forms up to this notion of equivalence.
Why quadratic forms?
Quadratic forms are a particularly natural type of object to try to classify. When I say “equivalence” of some sort of linear algebraic object defined on a vector space ![]() (over some field
(over some field ![]() ), one way of describing what this means is that
), one way of describing what this means is that ![]() naturally acts on these objects, and two such objects are equivalent iff some change of basis brings one to the other. Equivalence classes of these objects are thus the orbits of the action of
naturally acts on these objects, and two such objects are equivalent iff some change of basis brings one to the other. Equivalence classes of these objects are thus the orbits of the action of ![]() .
.
![]() is
is ![]() -dimensional, so if we have some
-dimensional, so if we have some ![]() -dimensional space of linear algebraic objects defined over
-dimensional space of linear algebraic objects defined over ![]() , then the space of equivalence classes of these objects is at least
, then the space of equivalence classes of these objects is at least ![]() -dimensional. So, if
-dimensional. So, if ![]() , then there will be infinitely many equivalence classes if
, then there will be infinitely many equivalence classes if ![]() is infinite, and even if
is infinite, and even if ![]() is finite, the number of equivalence classes will grow in proportion to some power of
is finite, the number of equivalence classes will grow in proportion to some power of ![]() .
.
For example, for large ![]() , the space of cubic forms, or symmetric trilinear forms, on
, the space of cubic forms, or symmetric trilinear forms, on ![]() is approximately
is approximately ![]() -dimensional, which is much greater than
-dimensional, which is much greater than ![]() , so the space of equivalence classes of symmetric trilinear forms is also approximately
, so the space of equivalence classes of symmetric trilinear forms is also approximately ![]() -dimensional, and counting cubic forms up to equivalence rather than individually barely cuts down the number of them at all, leaving us with no hope of a reasonable classification. The same issue kills pretty much any attempt to classify any type of tensor of rank at least 3.
-dimensional, and counting cubic forms up to equivalence rather than individually barely cuts down the number of them at all, leaving us with no hope of a reasonable classification. The same issue kills pretty much any attempt to classify any type of tensor of rank at least 3.
The space of (not necessarily symmetric) bilinear forms is ![]() -dimensional. But bilinear forms can be invariant under certain changes of coordinates, so the space of bilinear forms up to equivalence is still positive-dimensional. It isn’t enormously high-dimensional, like the space of cubic forms up to equivalence, so this doesn’t necessarily rule out any sort of reasonable classification (in fact, linear maps, which are also
-dimensional. But bilinear forms can be invariant under certain changes of coordinates, so the space of bilinear forms up to equivalence is still positive-dimensional. It isn’t enormously high-dimensional, like the space of cubic forms up to equivalence, so this doesn’t necessarily rule out any sort of reasonable classification (in fact, linear maps, which are also ![]() -dimensional, do have a reasonable classification. There’s the Jordan normal form for linear maps defined over algebraically closed fields, and the Frobenius normal form for arbitrary fields). But it does mean that any such classification isn’t going to be finitistic, like Sylvester’s law of inertia is.
-dimensional, do have a reasonable classification. There’s the Jordan normal form for linear maps defined over algebraically closed fields, and the Frobenius normal form for arbitrary fields). But it does mean that any such classification isn’t going to be finitistic, like Sylvester’s law of inertia is.
Classifying objects is also not too interesting if there’s very few of them for very straightforward reasons, and this tends to happen if there’s far fewer than ![]() of them, so that it’s too easy to change one to another by change of coordinates. For instance, the space of vectors is
of them, so that it’s too easy to change one to another by change of coordinates. For instance, the space of vectors is ![]() -dimensional, and there’s only two vectors up to equivalence: the zero vector, and the nonzero vectors.
-dimensional, and there’s only two vectors up to equivalence: the zero vector, and the nonzero vectors.
To get to the happy medium, where there’s a nontrivial zero-dimensional space of things up to equivalence, you want to start with some space of objects that’s just a bit less than ![]() -dimensional. Besides quadratic forms / symmetric bilinear forms, the only other obvious candidate is antisymmetric bilinear forms. But it turns out these are already fairly rigid. The argument about classifying symmetric bilinear forms reducing to classifying the nondegenerate ones applies to antisymmetric bilinear forms as well, and, up to equivalence, there’s not that many nondegenerate antisymmetric bilinear forms, also known as symplectic forms: Over any field, there’s only one of them in each even dimension, and none at all in odd dimensions.
-dimensional. Besides quadratic forms / symmetric bilinear forms, the only other obvious candidate is antisymmetric bilinear forms. But it turns out these are already fairly rigid. The argument about classifying symmetric bilinear forms reducing to classifying the nondegenerate ones applies to antisymmetric bilinear forms as well, and, up to equivalence, there’s not that many nondegenerate antisymmetric bilinear forms, also known as symplectic forms: Over any field, there’s only one of them in each even dimension, and none at all in odd dimensions.
Classification of quadratic forms over certain infinite fields
Let’s start with ![]() (though the following theorem and proof work just as well for any ordered field containing the square root of every positive element). We’ll use this same proof technique for other fields later.
(though the following theorem and proof work just as well for any ordered field containing the square root of every positive element). We’ll use this same proof technique for other fields later.
Theorem (Sylvester’s law of inertia): For an ![]() -dimensional nondegenerate real quadratic form
-dimensional nondegenerate real quadratic form ![]() , let
, let ![]() denote the maximum dimension of a subspace on which
denote the maximum dimension of a subspace on which ![]() takes only positive values, and let
takes only positive values, and let ![]() denote the maximum dimension of a subspace on which
denote the maximum dimension of a subspace on which ![]() takes only negative values. Then
takes only negative values. Then ![]() , and
, and ![]() is equivalent to the quadratic form represented by the diagonal matrix whose first
is equivalent to the quadratic form represented by the diagonal matrix whose first ![]() diagonal entries are
diagonal entries are ![]() and whose last
and whose last ![]() diagonal entries are
diagonal entries are ![]() . All pairs of nonnegative integers
. All pairs of nonnegative integers ![]() summing to
summing to ![]() are possible, and
are possible, and ![]() completely classifies nondegenerate real quadratic forms up to isomorphism. Thus, up to equivalence, there are exactly
completely classifies nondegenerate real quadratic forms up to isomorphism. Thus, up to equivalence, there are exactly ![]() nondegenerate
nondegenerate ![]() -dimensional real quadratic forms.
-dimensional real quadratic forms.
Proof: First we’ll show that every quadratic form can be diagonalized. We’ll use induction to build a basis ![]() in which a given quadratic form
in which a given quadratic form ![]() is diagonal. For the base case, it is trivially true that every
is diagonal. For the base case, it is trivially true that every ![]() -dimensional quadratic form can be diagonalized (and
-dimensional quadratic form can be diagonalized (and ![]() -dimensional quadratic forms are just as straightforwardly diagonalizable, if you prefer that as the base case). Now suppose every
-dimensional quadratic forms are just as straightforwardly diagonalizable, if you prefer that as the base case). Now suppose every ![]() -dimensional quadratic form is diagonalizable, and let
-dimensional quadratic form is diagonalizable, and let ![]() be an
be an ![]() -dimensional quadratic form. Let
-dimensional quadratic form. Let ![]() be any vector with
be any vector with ![]() (if this is not possible, then
(if this is not possible, then ![]() , and is represented by the zero matrix, which is diagonal). Then
, and is represented by the zero matrix, which is diagonal). Then ![]() is an
is an ![]() -dimensional subspace disjoint from
-dimensional subspace disjoint from ![]() . Using the induction hypothesis, let
. Using the induction hypothesis, let ![]() be a basis for
be a basis for ![]() in which
in which ![]() is diagonal. Then
is diagonal. Then ![]() is a basis in which
is a basis in which ![]() is diagonal (its matrix has
is diagonal (its matrix has ![]() in the upper left entry, the diagonal matrix representing
in the upper left entry, the diagonal matrix representing ![]() in the basis
in the basis ![]() in the submatrix that excludes the first row and column, and the fact that
in the submatrix that excludes the first row and column, and the fact that ![]() for
for ![]() means that the rest of the first row and column are zero).
means that the rest of the first row and column are zero).
Now that we’ve diagonalized ![]() , we can easily make those diagonal entries be
, we can easily make those diagonal entries be ![]() , assuming
, assuming ![]() is nondegenerate (otherwise, some of them will be
is nondegenerate (otherwise, some of them will be ![]() ). If
). If ![]() , then
, then ![]() . If
. If ![]() , then
, then ![]() . Either way, we can replace
. Either way, we can replace ![]() with some scalar multiple of it such that
with some scalar multiple of it such that ![]() .
.
The ordering of the diagonal entries doesn’t matter because we can permute the basis vectors so that all the ![]() ‘s come before all the
‘s come before all the ![]() ‘s. So all that remains to show is that any two quadratic forms whose
‘s. So all that remains to show is that any two quadratic forms whose ![]() diagonal matrices have different numbers of
diagonal matrices have different numbers of ![]() ‘s are not equivalent. Let
‘s are not equivalent. Let ![]() be the number of
be the number of ![]() ‘s and let
‘s and let ![]() be the number of
be the number of ![]() ‘s, so that our diagonalized quadratic form can be written as
‘s, so that our diagonalized quadratic form can be written as ![]() . There is an
. There is an ![]() -dimensional subspace
-dimensional subspace ![]() on which it only takes positive values (the subspace defined by
on which it only takes positive values (the subspace defined by ![]() ), and an
), and an ![]() -dimensional subspace
-dimensional subspace ![]() on which it only takes negative values (the subspace defined by
on which it only takes negative values (the subspace defined by ![]() ). It can’t have an
). It can’t have an ![]() -dimensional subspace on which it takes only positive values, because such a subspace would have to intersect
-dimensional subspace on which it takes only positive values, because such a subspace would have to intersect ![]() , and similarly, it can’t have an
, and similarly, it can’t have an ![]() -dimensional subspace on which it takes only negative values, because such a subspace would have to intersect
-dimensional subspace on which it takes only negative values, because such a subspace would have to intersect ![]() . Thus the number of
. Thus the number of ![]() ‘s and
‘s and ![]() ‘s are the maximum dimensions of subspaces on which the quadratic form takes only positive values and only negative values, respectively, and hence quadratic forms with different numbers of
‘s are the maximum dimensions of subspaces on which the quadratic form takes only positive values and only negative values, respectively, and hence quadratic forms with different numbers of ![]() ‘s are not equivalent.
‘s are not equivalent. ![]()
Over ![]() , things are simpler.
, things are simpler.
Theorem: All ![]() -dimensional nondegenerate complex quadratic forms are equivalent to each other.
-dimensional nondegenerate complex quadratic forms are equivalent to each other.
Proof: As in the real case, we can diagonalize any quadratic form; the proof of this did not depend on the field. But in ![]() , every number has a square root, so each basis vector
, every number has a square root, so each basis vector ![]() can be scaled by
can be scaled by ![]() , to get a vector that
, to get a vector that ![]() sends to
sends to ![]() (of course,
(of course, ![]() has two square roots, but you can just pick one of them arbitrarily). Thus every nondegenerate complex quadratic form is equivalent to the quadratic form defined by the identity matrix.
has two square roots, but you can just pick one of them arbitrarily). Thus every nondegenerate complex quadratic form is equivalent to the quadratic form defined by the identity matrix. ![]()
Note that this proof works just as well over any quadratically closed field not of characteristic 2.
Over other fields, things get a bit complicated. One class of fields you might want to consider is the p-adic numbers, and there is a known classification (called the Hasse invariant) of quadratic forms over ![]() (and its finite extensions), but it involves Brauer groups, for some reason.
(and its finite extensions), but it involves Brauer groups, for some reason.
Over the rationals, things are even worse. The best result about classifying rational quadratic forms we have is the Hasse-Minkowski theorem: Over any finite extension of ![]() , two quadratic forms are equivalent iff they are equivalent over every non-discrete completion of the field (so, they are equivalent over
, two quadratic forms are equivalent iff they are equivalent over every non-discrete completion of the field (so, they are equivalent over ![]() itself iff they are equivalent over
itself iff they are equivalent over ![]() and over
and over ![]() for every prime
for every prime ![]() ). An interesting result, but not one that lets you easily list out equivalence classes of rational quadratic forms.
). An interesting result, but not one that lets you easily list out equivalence classes of rational quadratic forms.
But over finite fields, things go back to being relatively straightforward.
Classification of nondegenerate quadratic forms over finite fields of odd characteristic
Let ![]() be a power of an odd prime, and let
be a power of an odd prime, and let ![]() denote the field with
denote the field with ![]() elements.
elements.
![]() has a certain feature in common with
has a certain feature in common with ![]() : exactly half of its nonzero elements are squares. For
: exactly half of its nonzero elements are squares. For ![]() , you can show this with a counting argument: every nonzero square is the square of exactly two nonzero elements, and there are finitely many nonzero elements. For
, you can show this with a counting argument: every nonzero square is the square of exactly two nonzero elements, and there are finitely many nonzero elements. For ![]() , it might not be obvious how to formally make sense of the claim that exactly half of nonzero reals are squares (i.e. positive). One way is to notice that the positive reals and negative reals are isomorphic as topological spaces. But what matters in this context is that the quotient group
, it might not be obvious how to formally make sense of the claim that exactly half of nonzero reals are squares (i.e. positive). One way is to notice that the positive reals and negative reals are isomorphic as topological spaces. But what matters in this context is that the quotient group ![]() has order
has order ![]() , just like
, just like ![]() (here
(here ![]() means the group of units of a field
means the group of units of a field ![]() ). Now let’s see how this relates to quadratic forms.
). Now let’s see how this relates to quadratic forms.
The part of the proof of Sylvester’s law of inertia that shows that every nondegenerate real symmetric form can be diagonalized with diagonal elements ![]() can be generalized to an arbitrary field:
can be generalized to an arbitrary field:
Lemma 1: Let ![]() be a field, and let
be a field, and let ![]() be a set of elements of
be a set of elements of ![]() consisting of one element from each coset of
consisting of one element from each coset of ![]() . Then every nondegenerate quadratic form over
. Then every nondegenerate quadratic form over ![]() is equivalent to one represented by a diagonal matrix with elements of
is equivalent to one represented by a diagonal matrix with elements of ![]() on the diagonal.
on the diagonal.
Proof: As in the proof of Sylvester’s law of inertia, with ![]() replaced with the set
replaced with the set ![]() .
. ![]()
Since ![]() has exactly 2 cosets in
has exactly 2 cosets in ![]() , this means there is a set
, this means there is a set ![]() of size
of size ![]() (if
(if ![]() , then
, then ![]() is nonsquare, and you could use
is nonsquare, and you could use ![]() again) such that every
again) such that every ![]() -dimensional nondegenerate quadratic form over
-dimensional nondegenerate quadratic form over ![]() is equivalent to one represented by a diagonal matrix with elements of
is equivalent to one represented by a diagonal matrix with elements of ![]() on the diagonal, and thus there are at most
on the diagonal, and thus there are at most ![]() of them up to equivalence. However, we have not shown that these quadratic forms are inequivalent to each other (that part of the proof of Sylvester’s law of inertia used the fact that
of them up to equivalence. However, we have not shown that these quadratic forms are inequivalent to each other (that part of the proof of Sylvester’s law of inertia used the fact that ![]() is ordered), and in fact, this is not the case. Instead, the following lower bound ends up being tight over finite fields of odd characteristic:
is ordered), and in fact, this is not the case. Instead, the following lower bound ends up being tight over finite fields of odd characteristic:
Lemma 2: Let ![]() be a field. Any two invertible symmetric matrices whose determinants are in different cosets of
be a field. Any two invertible symmetric matrices whose determinants are in different cosets of ![]() represent inequivalent quadratic forms (that is, if their determinants are
represent inequivalent quadratic forms (that is, if their determinants are ![]() and
and ![]() , and
, and ![]() is nonsquare, then the matrices do not represent equivalent quadratic forms). Thus, for
is nonsquare, then the matrices do not represent equivalent quadratic forms). Thus, for ![]() , there are at least
, there are at least ![]() nondegenerate
nondegenerate ![]() -dimensional quadratic forms over
-dimensional quadratic forms over ![]() up to equivalence.
up to equivalence.
Proof: If invertible symmetric matrices ![]() and
and ![]() represent equivalent quadratic forms, then there is some change of basis matrix
represent equivalent quadratic forms, then there is some change of basis matrix ![]() such that
such that ![]() .
. ![]() . If
. If ![]() , then for every element of
, then for every element of ![]() , there is a symmetric matrix that has that determinant, so the fact that symmetric matrices whose determinants are in different cosets of
, there is a symmetric matrix that has that determinant, so the fact that symmetric matrices whose determinants are in different cosets of ![]() represent inequivalent quadratic forms implies that there are inequivalent nondegenerate quadratic forms for each coset.
represent inequivalent quadratic forms implies that there are inequivalent nondegenerate quadratic forms for each coset. ![]()
What’s going on here is that there’s a notion of the determinant of a bilinear form that doesn’t depend on a matrix representing it in some basis. For every ![]() -dimensional vector space
-dimensional vector space ![]() , there’s an associated
, there’s an associated ![]() -dimensional vector space
-dimensional vector space ![]() , called the space of volume forms on
, called the space of volume forms on ![]() . Elements of
. Elements of ![]() are called volume forms because, over
are called volume forms because, over ![]() , they represent amounts of volume (with orientation) of regions in the vector space. This is not exactly a scalar, but rather an element of a different
, they represent amounts of volume (with orientation) of regions in the vector space. This is not exactly a scalar, but rather an element of a different ![]() -dimensional vector space, because, in a pure vector space (without any additional structure like an inner product), there’s no way to say how much volume is
-dimensional vector space, because, in a pure vector space (without any additional structure like an inner product), there’s no way to say how much volume is ![]() . I won’t give the definition here, but anyway, a bilinear form
. I won’t give the definition here, but anyway, a bilinear form ![]() on a vector space
on a vector space ![]() induces a bilinear form
induces a bilinear form ![]() on
on ![]() . A basis for
. A basis for ![]() induces a basis for
induces a basis for ![]() , in which
, in which ![]() is represented by a
is represented by a ![]() matrix (i.e. scalar) that is the determinant of the matrix representing
matrix (i.e. scalar) that is the determinant of the matrix representing ![]() . An automorphism
. An automorphism ![]() of
of ![]() induces an automorphism of
induces an automorphism of ![]() , which is multiplication by
, which is multiplication by ![]() , and thus induces an automorphism of the space of bilinear forms on
, and thus induces an automorphism of the space of bilinear forms on ![]() given by division by
given by division by ![]() . Thus if the ratio of the determinants of two nondegenerate bilinear forms is not a square, then the bilinear forms cannot be equivalent. This also applies to quadratic forms, using their correspondence to symmetric bilinear forms.
. Thus if the ratio of the determinants of two nondegenerate bilinear forms is not a square, then the bilinear forms cannot be equivalent. This also applies to quadratic forms, using their correspondence to symmetric bilinear forms.
Theorem: Up to equivalence, there are exactly two ![]() -dimensional nondegenerate quadratic forms over
-dimensional nondegenerate quadratic forms over ![]() (for
(for ![]() ).
).
Proof: Lemma 2 implies that invertible symmetric matrices of square determinant and invertible symmetric matices of nonsquare determinant represent inequivalent quadratic forms. It remains to show that any two invertible symmetric matrices with either both square determinant or both nonsquare determinant represent equivalent quadratic forms.
Let ![]() be square, and nonsquare, respectively. By lemma 1, every nondegenerate quadratic form over
be square, and nonsquare, respectively. By lemma 1, every nondegenerate quadratic form over ![]() can be represented with a diagonal matrix whose diagonal entries are all
can be represented with a diagonal matrix whose diagonal entries are all ![]() or
or ![]() . The determinant is square iff an even number of diagonal entries are
. The determinant is square iff an even number of diagonal entries are ![]() . It suffices to show that changing two
. It suffices to show that changing two ![]() ‘s into
‘s into ![]() ‘s or vice-versa doesn’t change the equivalence class of the quadratic form being represented. Thus this reduces the problem to show that the
‘s or vice-versa doesn’t change the equivalence class of the quadratic form being represented. Thus this reduces the problem to show that the ![]() -dimensional quadratic forms represented by
-dimensional quadratic forms represented by ![]() and
and ![]() are equivalent. If we can find
are equivalent. If we can find ![]() such that
such that ![]() , then the change of basis matrix
, then the change of basis matrix ![]() will do, because
will do, because ![]() . This reduces the problem to showing that there are such
. This reduces the problem to showing that there are such ![]() .
.
The squares in ![]() cannot be an additive subgroup of
cannot be an additive subgroup of ![]() , because there are
, because there are ![]() of them, which does not divide
of them, which does not divide ![]() . Thus there are
. Thus there are ![]() such that
such that ![]() is nonsquare. Since
is nonsquare. Since ![]() has order
has order ![]() , and
, and ![]() is also nonsquare, it follows that
is also nonsquare, it follows that ![]() is a square. Let
is a square. Let ![]() , and let
, and let ![]() and
and ![]() . Then
. Then ![]() , as desired.
, as desired. ![]()
Note, as a consequence, if we count the degenerate quadratic forms as well, there are ![]()
![]() -dimensional quadratic forms over
-dimensional quadratic forms over ![]() up to equivalence:
up to equivalence: ![]() for every positive dimension that’s at most
for every positive dimension that’s at most ![]() , and
, and ![]() more for dimension
more for dimension ![]() (this is the zero quadratic form; there are no zero-dimensional quadratic forms of nonsquare determinant).
(this is the zero quadratic form; there are no zero-dimensional quadratic forms of nonsquare determinant).
Counting
Given an ![]() -dimensional quadratic form
-dimensional quadratic form ![]() over
over ![]() , and some scalar
, and some scalar ![]() , how many vectors
, how many vectors ![]() are there such that
are there such that ![]() ? There are
? There are ![]() vectors
vectors ![]() , and
, and ![]() possible values of
possible values of ![]() , so, on average, there will be
, so, on average, there will be ![]() vectors with any given value for the quadratic form, but let’s look more precisely.
vectors with any given value for the quadratic form, but let’s look more precisely.
First, note that we don’t have to check every quadratic form individually, because if two quadratic forms are equivalent, then for any given scalar ![]() , each form will assign value
, each form will assign value ![]() to the same number of vectors. And it’s enough to check nondegenerate forms, because every quadratic form on a vector space
to the same number of vectors. And it’s enough to check nondegenerate forms, because every quadratic form on a vector space ![]() corresponds to a nondegenerate quadratic form on some quotient
corresponds to a nondegenerate quadratic form on some quotient ![]() , and the number of vectors it assigns a given value is just
, and the number of vectors it assigns a given value is just ![]() times the number of vectors the corresponding nondegenerate quadratic form assigns the same value. So we just have to check 2 quadratic forms of each dimension.
times the number of vectors the corresponding nondegenerate quadratic form assigns the same value. So we just have to check 2 quadratic forms of each dimension.
And we don’t have to check all ![]() scalars individually because, if
scalars individually because, if ![]() is a square, then multiplication by its square root is a bijection between
is a square, then multiplication by its square root is a bijection between ![]() and
and ![]() . So there’s only
. So there’s only ![]() cases to check:
cases to check: ![]() ,
, ![]() is a nonzero square, or
is a nonzero square, or ![]() is nonsquare. If the dimension is even, there’s even fewer cases, because a quadratic form is equivalent to any nonzero scalar multiple of it, so each nonzero scalar
is nonsquare. If the dimension is even, there’s even fewer cases, because a quadratic form is equivalent to any nonzero scalar multiple of it, so each nonzero scalar ![]() has the same number of vectors that
has the same number of vectors that ![]() sends to
sends to ![]() . Thus, for any
. Thus, for any ![]() -dimensional quadratic form
-dimensional quadratic form ![]() , there will be some number
, there will be some number ![]() such that, for each
such that, for each ![]() ,
, ![]() , and
, and ![]() .
.
And it turns out that in odd dimensions, for any nonzero quadratic form ![]() , the probability that
, the probability that ![]() for a randomly selected vector
for a randomly selected vector ![]() is exactly
is exactly ![]() . To see this, we can reduce to the
. To see this, we can reduce to the ![]() -dimensional case (which is clear because there’s
-dimensional case (which is clear because there’s ![]() vectors and only
vectors and only ![]() gets sent to
gets sent to ![]() by
by ![]() ): Given a
): Given a ![]() -dimensional quadratic form
-dimensional quadratic form ![]() , let
, let ![]() be a
be a ![]() -dimensional subspace on which
-dimensional subspace on which ![]() is nonzero, and let
is nonzero, and let ![]() . Then every vector is uniquely a sum
. Then every vector is uniquely a sum ![]() for some
for some ![]() and
and ![]() , and
, and ![]() . Since
. Since ![]() is a quadratic form on the
is a quadratic form on the ![]() -dimensional space
-dimensional space ![]() , there’s some number
, there’s some number ![]() such that for each
such that for each ![]() ,
, ![]() , and
, and ![]() . For
. For ![]() and
and ![]() ,
, ![]() iff
iff ![]() (
(![]() ways for this to happen) or
ways for this to happen) or ![]() (
(![]() ways for this to happen), for a total of
ways for this to happen), for a total of ![]() vectors
vectors ![]() such that
such that ![]() . Since there’s the same number of nonzero squares as nonsquares, it follows that there is some number
. Since there’s the same number of nonzero squares as nonsquares, it follows that there is some number ![]() such that for each
such that for each ![]() ,
, ![]() if
if ![]() is square, and
is square, and ![]() if
if ![]() is nonsquare.
is nonsquare.
We can compute these offsets ![]() and
and ![]() recursively. We can represent quadratic forms of square determinant with the identity matrix (i.e.
recursively. We can represent quadratic forms of square determinant with the identity matrix (i.e. ![]() ). The number of vectors
). The number of vectors ![]() such that
such that ![]() is
is ![]() . (Why do I suggest decrementing
. (Why do I suggest decrementing ![]() by
by ![]() at a time? You could also try decrementing
at a time? You could also try decrementing ![]() by
by ![]() each step, but I think
each step, but I think ![]() is easier because of the significance of the parity of the dimension). We can represent quadratic forms of nonsquare determinant with a matrix that is the identity except for the last diagonal entry being replaced with a nonsquare, and then compute how many vectors it assigns each scalar in terms of the square-determinant quadratic forms of one lower dimension.
is easier because of the significance of the parity of the dimension). We can represent quadratic forms of nonsquare determinant with a matrix that is the identity except for the last diagonal entry being replaced with a nonsquare, and then compute how many vectors it assigns each scalar in terms of the square-determinant quadratic forms of one lower dimension.
It turns out that it matters whether ![]() is a square in
is a square in ![]() . To see this, consider the case of a
. To see this, consider the case of a ![]() -dimensional quadratic form of square determinant:
-dimensional quadratic form of square determinant: ![]() , and let’s see how many solutions there are to
, and let’s see how many solutions there are to ![]() . Assuming
. Assuming ![]() is nonzero,
is nonzero, ![]() iff
iff ![]() . If
. If ![]() is not a square, then this is not possible, so
is not a square, then this is not possible, so ![]() is the only solution. But if
is the only solution. But if ![]() is a square, then it has two square roots that
is a square, then it has two square roots that ![]() could be, and
could be, and ![]() choices of overall scale, so there’s
choices of overall scale, so there’s ![]() nonzero solutions, and thus
nonzero solutions, and thus ![]() total solutions.
total solutions. ![]() is a square iff
is a square iff ![]() , so we can phrase this as that it matters whether
, so we can phrase this as that it matters whether ![]() is
is ![]() or
or ![]()
![]() .
.
If you state and solve the recurrence, you should find that: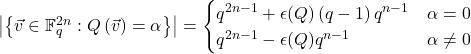
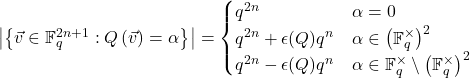
Where ![]() is defined as follows:
is defined as follows:
If ![]() , then
, then ![]() if
if ![]() has square determinant, and
has square determinant, and ![]() if
if ![]() has nonsquare determinant.
has nonsquare determinant.
If ![]() , then
, then ![]() is defined as in the previous case if
is defined as in the previous case if ![]() is even, but is reversed if
is even, but is reversed if ![]() is odd. Remember that the dimensions above were
is odd. Remember that the dimensions above were ![]() and
and ![]() , so, by
, so, by ![]() , I mean half the dimension (rounded down).
, I mean half the dimension (rounded down).
It turns out that counting how many vectors a quadratic form assigns each value is useful for another counting problem: Now we can determine the order of the automorphism group of a quadratic form.
If ![]() is an
is an ![]() -dimensional quadratic form of square determinant, it can be represented by the identity matrix. A matrix with columns
-dimensional quadratic form of square determinant, it can be represented by the identity matrix. A matrix with columns ![]() is an automorphism of
is an automorphism of ![]() iff
iff ![]() and
and ![]() for
for ![]() . Once
. Once ![]() have been chosen, the space that’s
have been chosen, the space that’s ![]() -orthogonal to all of them is
-orthogonal to all of them is ![]() -dimensional, and
-dimensional, and ![]() restricts to a quadratic form on it of square determinant, so the number of options for
restricts to a quadratic form on it of square determinant, so the number of options for ![]() is the number of vectors that an
is the number of vectors that an ![]() -dimensional quadratic form of square determinant assigns value
-dimensional quadratic form of square determinant assigns value ![]() (which is square). Thus the order of the automorphism group of
(which is square). Thus the order of the automorphism group of ![]() is the product of these over all
is the product of these over all ![]() .
.
If ![]() is an
is an ![]() -dimensional quadratic form of nonsquare determinant, we can do a similar thing, representing
-dimensional quadratic form of nonsquare determinant, we can do a similar thing, representing ![]() with a matrix like the identity, but with the first diagonal entry replaced with a nonsquare. Then the number of options for
with a matrix like the identity, but with the first diagonal entry replaced with a nonsquare. Then the number of options for ![]() is the number of vectors that a quadratic form of nonsquare determinant assigns some particular nonsquare value, and the rest of the product is unchanged.
is the number of vectors that a quadratic form of nonsquare determinant assigns some particular nonsquare value, and the rest of the product is unchanged.
If you evaluate these products, you should get:![]() :
: ![]()
![]() :
: ![]()
You may notice that, in odd dimensions, the size of the automorphism group of a quadratic form does not depend on its determinant. In fact, the groups are the same. This is because multiplication by a nonsquare scalar sends a quadratic form of square determinant to a quadratic form of nonsquare determinant, and does not change its automorphism group.
As a sanity check, ![]() is a subgroup of the general linear group, so its order should divide the order of the general linear group.
is a subgroup of the general linear group, so its order should divide the order of the general linear group. ![]() (which can be shown with a similar recursive computation). And indeed:
(which can be shown with a similar recursive computation). And indeed:
![]() :
: ![]()
![]() :
: ![]()
By the orbit-stabilizer theorem, these count the number of quadratic forms of each equivalence class.
The sum of the sizes of the two equivalence classes is the total number of (individual, not up to equivalence) nondegenerate quadratic forms on a vector space, or equivalently, the number of invertible symmetric matrices. This sum is![]() :
: ![]()
![]() :
: ![]()
The leading terms of these are ![]() and
and ![]() , respectively, which are the numbers of symmetric
, respectively, which are the numbers of symmetric ![]() and
and ![]() matrices, respectively. And the second terms of each are negative, which makes sense because we’re excluding singular matrices. You could compute the sizes of all equivalence classes of quadratic forms on an
matrices, respectively. And the second terms of each are negative, which makes sense because we’re excluding singular matrices. You could compute the sizes of all equivalence classes of quadratic forms on an ![]() -dimensional vector space, not just the nondegenerate ones, and add them up, and you should get exactly
-dimensional vector space, not just the nondegenerate ones, and add them up, and you should get exactly ![]() .
.
Fields of well-defined Euler characteristic
![]() is, of course, infinite, but if you had to pick a finite number that acts most like the size of
is, of course, infinite, but if you had to pick a finite number that acts most like the size of ![]() , it turns out that
, it turns out that ![]() is a decent answer in some ways. After all,
is a decent answer in some ways. After all, ![]() and
and ![]() each are homeomorphic to
each are homeomorphic to ![]() , so they should probably all have the same size, and
, so they should probably all have the same size, and ![]() ;
; ![]() has size
has size ![]() , and size should probably be additive, which would imply that, if we’re denoting the “size” of
, and size should probably be additive, which would imply that, if we’re denoting the “size” of ![]() by
by ![]() ,
, ![]() , which implies
, which implies ![]() . Then, of course,
. Then, of course, ![]() should have “size”
should have “size” ![]() .
.
This might seem silly, but it’s deeper than it sounds. This notion of “size” is called Euler characteristic (this is actually different from what algebraic topologists call Euler characteristic, though it’s the same for compact manifolds). A topological space ![]() has an Euler characteristic, denoted
has an Euler characteristic, denoted ![]() , if it can be partitioned into finitely many cells, each of which is homeomorphic to
, if it can be partitioned into finitely many cells, each of which is homeomorphic to ![]() for some
for some ![]() . If
. If ![]() can be partitioned into cells
can be partitioned into cells ![]() , and
, and ![]() is homeomorphic to
is homeomorphic to ![]() , then
, then ![]() and
and ![]() . This is well-defined, in the sense that multiple different ways of partitioning a space into cells that are homeomorphic to
. This is well-defined, in the sense that multiple different ways of partitioning a space into cells that are homeomorphic to ![]() will give you the same Euler characteristic. Roughly speaking, this is because partitions of a space can be refined by splitting an
will give you the same Euler characteristic. Roughly speaking, this is because partitions of a space can be refined by splitting an ![]() -dimensional cell into two
-dimensional cell into two ![]() -dimensional cells and the
-dimensional cells and the ![]() -dimensional boundary between them, this does not change the Euler characteristic, and any two partitions into cells have a common refinement.
-dimensional boundary between them, this does not change the Euler characteristic, and any two partitions into cells have a common refinement.
Euler characteristic has a lot in common with sizes of finite sets, and is, in some ways, a natural generalization of it. For starters, the Euler characteristic of any finite set is its size. Some familiar properties of sizes of sets generalize to Euler characteristics, such as ![]() , and
, and ![]() .
.
In fact, all of the counting problems we just did over finite fields of odd size applies just as well to fields of well-defined odd Euler characteristic. There are only two infinite fields that have an Euler characteristic: ![]() , with
, with ![]() , and
, and ![]() , with
, with ![]() .
.
Recall that in the counting problems in the previous section, we needed to know whether or not ![]() contains a square root of
contains a square root of ![]() , and that it does iff
, and that it does iff ![]() . This extends to fields with Euler characteristic just fine, since
. This extends to fields with Euler characteristic just fine, since ![]() and
and ![]() contains a square root of
contains a square root of ![]() , and
, and ![]() and
and ![]() does not contain a square root of
does not contain a square root of ![]() . In fact, this generalizes a bit.
. In fact, this generalizes a bit. ![]() contains the primitive
contains the primitive ![]() th roots of unity iff
th roots of unity iff ![]() .
. ![]() for every
for every ![]() , and
, and ![]() contains all roots of unity.
contains all roots of unity. ![]() only for
only for ![]() and
and ![]() , and the only roots of unity in
, and the only roots of unity in ![]() are
are ![]() itself and its primitive square root
itself and its primitive square root ![]() .
.
Anyway, let’s start with positive-definite real quadratic forms (i.e. those only taking positive values). If ![]() is an
is an ![]() -dimensional positive-definite real quadratic form, then
-dimensional positive-definite real quadratic form, then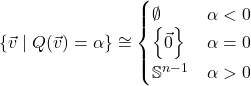
For negative-definite quadratic forms, of course, the positive and negative cases switch.
Now let’s try the indefinite quadratic forms. Recall that for every nondegenerate quadratic form ![]() on a real vector space
on a real vector space ![]() , there are
, there are ![]() -orthogonal subspaces
-orthogonal subspaces ![]() such that
such that ![]() is positive-definite,
is positive-definite, ![]() is negative-definite, and
is negative-definite, and ![]() . Let
. Let ![]() and
and ![]() . For
. For ![]() , in order for
, in order for ![]() to satisfy
to satisfy ![]() ,
, ![]() can be anything, and then
can be anything, and then ![]() must lie on the
must lie on the ![]() -dimensional sphere
-dimensional sphere ![]() . If
. If ![]() , then
, then ![]() and
and ![]() switch roles. In order for
switch roles. In order for ![]() to satisfy
to satisfy ![]() , either
, either ![]() , or there’s some
, or there’s some ![]() such that
such that ![]() lies on the
lies on the ![]() -dimensional sphere
-dimensional sphere ![]() and
and ![]() lies on the
lies on the ![]() -dimensional sphere
-dimensional sphere ![]() . Thus
. Thus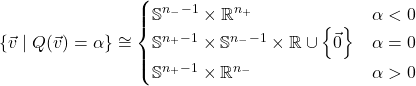
With ![]() , this also works for definite quadratic forms.
, this also works for definite quadratic forms.
If you remove one point from ![]() , you get
, you get ![]() , so
, so ![]() ; that is,
; that is, ![]() if
if ![]() is even, and
is even, and ![]() if
if ![]() is odd. Thus the Euler characteristics of the above level sets of
is odd. Thus the Euler characteristics of the above level sets of ![]() depend only on the parities of
depend only on the parities of ![]() and
and ![]() . The parity of
. The parity of ![]() is equivalent to the sign of
is equivalent to the sign of ![]() , and
, and ![]() is the dimension. So the Euler characteristics of the level sets of
is the dimension. So the Euler characteristics of the level sets of ![]() depend only on the parity of its dimension and the sign of its determinant, and
depend only on the parity of its dimension and the sign of its determinant, and![]() :
: 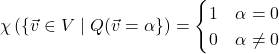
![]() :
: 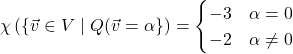
![]() :
: 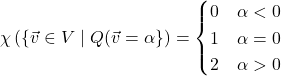
![]() :
: 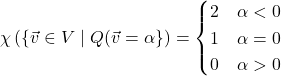
In comparison, if you take our earlier formula for the sizes of these level sets over ![]() and plug in
and plug in ![]() , you get
, you get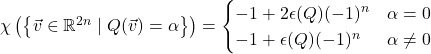
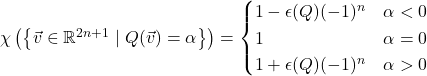
![]() is the sign of the determinant, so these two calculations agree.
is the sign of the determinant, so these two calculations agree.
Now let’s look at complex quadratic forms. Since every complex number is square and ![]() ,
, ![]() for every nondegenerate complex quadratic form
for every nondegenerate complex quadratic form ![]() . Thus our formulas for sizes of level sets of quadratic forms over finite fields predicts
. Thus our formulas for sizes of level sets of quadratic forms over finite fields predicts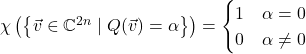
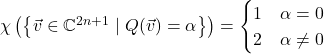
In the odd-dimensional case, I’ve left out the nonsquare case, and relabeled the case where ![]() is a nonzero square as
is a nonzero square as ![]() , because all complex numbers are squares.
, because all complex numbers are squares.
It’s easy to verify that the zero-sets of complex quadratic forms have Euler characteristic ![]() . This is because, besides the origin, all of the other solutions to
. This is because, besides the origin, all of the other solutions to ![]() can be arbitrarily rescaled to get more solutions, and
can be arbitrarily rescaled to get more solutions, and ![]() . That is, let
. That is, let ![]() be the space of
be the space of ![]() -dimensional subspaces on which
-dimensional subspaces on which ![]() is zero. Then
is zero. Then ![]() , so
, so ![]() .
.
The Euler characteristics of the other level sets of complex quadratic forms can be checked by induction. A ![]() -dimensional quadratic form takes no nonzero values, so
-dimensional quadratic form takes no nonzero values, so ![]() . An
. An ![]() -dimensional quadratic form
-dimensional quadratic form ![]() can be diagonalized as
can be diagonalized as ![]() . For
. For ![]() , the solutions to
, the solutions to ![]() can be partitioned into three pieces:
can be partitioned into three pieces:
1. ![]() . This has Euler characteristic
. This has Euler characteristic ![]() .
.
2. ![]() . This has Euler characteristic
. This has Euler characteristic ![]() .
.
3. For some ![]() ,
, ![]() . This has Euler characteristic
. This has Euler characteristic![]() (I’ve replaced
(I’ve replaced ![]() and
and ![]() with
with ![]() where they appear, since both are nonzero, and all the nonzero level sets are homeomorphic).
where they appear, since both are nonzero, and all the nonzero level sets are homeomorphic).
Thus, summing these up, we get ![]() , explaining the alternation between
, explaining the alternation between ![]() and
and ![]() .
.
There are some apparent disanalogies between finite fields and infinite fields with Euler characteristics. For instance, it is not true that exactly half of nonzero complex numbers are squares, at least in the sense that ![]() . However, it is still true (vacuously) that the ratio between any two nonsquare complex numbers is square. And the spaces of nonzero square and nonsquare complex numbers have the same Euler characteristic, since
. However, it is still true (vacuously) that the ratio between any two nonsquare complex numbers is square. And the spaces of nonzero square and nonsquare complex numbers have the same Euler characteristic, since ![]() . This had to be the case, because sufficiently non-pathological bijections preserve Euler characteristic, so sufficiently non-pathological two-to-one maps cut Euler characteristic in half, since the domain can be partitioned into two pieces in non-pathological bijection with the range.
. This had to be the case, because sufficiently non-pathological bijections preserve Euler characteristic, so sufficiently non-pathological two-to-one maps cut Euler characteristic in half, since the domain can be partitioned into two pieces in non-pathological bijection with the range.
And, while finite fields of odd characteristic have two nondegenerate ![]() -dimensional quadratic forms up to equivalence,
-dimensional quadratic forms up to equivalence, ![]() has just one, and
has just one, and ![]() has
has ![]() of them.
of them. ![]() ‘s missing second nondegenerate quadratic form of each dimension can be addressed similarly to its missing nonsquare elements. The number of nondegenerate
‘s missing second nondegenerate quadratic form of each dimension can be addressed similarly to its missing nonsquare elements. The number of nondegenerate ![]() -dimensional quadratic forms over
-dimensional quadratic forms over ![]() in each equivalence class is a multiple of
in each equivalence class is a multiple of ![]() , so, with
, so, with ![]() , this correctly predicts that the Euler characteristic of each equivalence class of
, this correctly predicts that the Euler characteristic of each equivalence class of ![]() -dimensional complex quadratic form is
-dimensional complex quadratic form is ![]() , and one of the equivalence classes being empty is consistent with that.
, and one of the equivalence classes being empty is consistent with that.
The oversupply of equivalence classes of real quadratic forms is a little subtler. Our analysis of nondegenerate quadratic forms over finite fields of odd characteristic predicts that any two nondegenerate real quadratic forms whose determinants have the same sign should be equivalent, and this is not the case. To address this, let’s look at the heap of isomorphisms between two nondegenerate quadratic forms whose determinants have the same sign. A heap is like a group that has forgotten its identity element. The heap of isomorphisms between two isomorphic objects is the underlying heap of the automorphism group of one of them. In particular, if the automorphism group of some object is a Lie group, then the heap of isomorphisms between it and another object it is isomorphic to is homeomorphic to the automorphism group, and thus they have the same Euler characteristic. In the finite case, this is just saying that the heap of isomorphisms between two isomorphic objects has the same size as the automorphism group of one of them. So when we computed the sizes of automorphism groups of nondegenerate quadratic forms over ![]() , we were also computing sizes of isomorphism heaps between isomorphic pairs of nondegenerate quadratic forms over
, we were also computing sizes of isomorphism heaps between isomorphic pairs of nondegenerate quadratic forms over ![]() . Plugging in
. Plugging in ![]() , this should also tell us the Euler characteristic of the heap of isomorphisms between two real quadratic forms whose determinants have the same sign. Notice that (with the exception of the cases where
, this should also tell us the Euler characteristic of the heap of isomorphisms between two real quadratic forms whose determinants have the same sign. Notice that (with the exception of the cases where ![]() and
and ![]() , or where
, or where ![]() ), the order of the automorphism group of a nondegenerate quadratic form over
), the order of the automorphism group of a nondegenerate quadratic form over ![]() is a multiple of
is a multiple of ![]() , so plugging in
, so plugging in ![]() predicts that the automorphism group of a nondegenerate real quadratic form has Euler characteristic
predicts that the automorphism group of a nondegenerate real quadratic form has Euler characteristic ![]() , and hence so does the heap of isomorphisms between two nondegenerate real quadratic forms of the same dimension whose determinants have the same sign. This is consistent with said heap of isomorphisms being empty! The exceptions, the quadratic forms whose automorphism groups do not have Euler characteristic
, and hence so does the heap of isomorphisms between two nondegenerate real quadratic forms of the same dimension whose determinants have the same sign. This is consistent with said heap of isomorphisms being empty! The exceptions, the quadratic forms whose automorphism groups do not have Euler characteristic ![]() , are when
, are when ![]() and
and ![]() , or when
, or when ![]() . These are exactly the cases when knowing the dimension of a nondegenerate real quadratic form and the sign of its determinant actually does tell you what the quadratic form is up to equivalence.
. These are exactly the cases when knowing the dimension of a nondegenerate real quadratic form and the sign of its determinant actually does tell you what the quadratic form is up to equivalence.
![Rendered by QuickLaTeX.com \left\langle \left[\begin{array}{c} t_{1}\\ x_{1}\\ y_{1}\\ z_{1} \end{array}\right],\left[\begin{array}{c} t_{2}\\ x_{2}\\ y_{2}\\ z_{2} \end{array}\right]\right\rangle =-c^{2}t_{1}t_{2}+x_{1}x_{2}+y_{1}y_{2}+z_{1}z_{1}](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-3f69ac65dafced1956311fcc8ca7ad7d_l3.png) . As a map
. As a map ![Rendered by QuickLaTeX.com \left[\begin{array}{c} t\\ x\\ y\\ z \end{array}\right]\mapsto\left[\begin{array}{cccc} -c^{2}t & x & y & z\end{array}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-72e747f3cc3e89f291d8ec1e182e0411_l3.png) . The inverse map
. The inverse map ![Rendered by QuickLaTeX.com \left[\begin{array}{cccc} \tau & \alpha & \beta & \gamma\end{array}\right]\mapsto\left[\begin{array}{c} -c^{-2}\tau\\ \alpha\\ \beta\\ \gamma \end{array}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-ca3ccd11aae199844acb1b6fc086afce_l3.png) , or, as an inner product on
, or, as an inner product on ![Rendered by QuickLaTeX.com \left\langle \left[\begin{array}{c} t_{1}\\ x_{1}\\ y_{1}\\ z_{1} \end{array}\right],\left[\begin{array}{c} t_{2}\\ x_{2}\\ y_{2}\\ z_{2} \end{array}\right]\right\rangle =-t_{1}t_{2}+c^{-2}x_{1}x_{2}+c^{-2}y_{1}y_{2}+c^{-2}z_{1}z_{1}](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-af984de58ef446b9c213959ef4a85274_l3.png) , or, as a map
, or, as a map ![Rendered by QuickLaTeX.com \left[\begin{array}{c} t\\ x\\ y\\ z \end{array}\right]\mapsto\left[\begin{array}{cccc} -t & c^{-2}x & c^{-2}y & c^{-2}z\end{array}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-164bacb88351b209a71b5d0ae60f4eda_l3.png) . The limit
. The limit ![Rendered by QuickLaTeX.com \left\langle \left[\begin{array}{c} t_{1}\\ x_{1}\\ y_{1}\\ z_{1} \end{array}\right],\left[\begin{array}{c} t_{2}\\ x_{2}\\ y_{2}\\ z_{2} \end{array}\right]\right\rangle =-t_{1}t_{2}](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-7d81eb8a4fb8e8e88bad52901712cbb6_l3.png) , and our spatial inner product on the dual space
, and our spatial inner product on the dual space ![Rendered by QuickLaTeX.com \left[\begin{array}{c} t\\ x\\ y\\ z \end{array}\right]\mapsto\left[\begin{array}{cccc} -t & 0 & 0 & 0\end{array}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-98d00b56bab5ecb597bd27c98b56d60a_l3.png) and
and ![Rendered by QuickLaTeX.com \left[\begin{array}{cccc} \tau & \alpha & \beta & \gamma\end{array}\right]\mapsto\left[\begin{array}{c} 0\\ \alpha\\ \beta\\ \gamma \end{array}\right]](http://alexmennen.com/wp-content/ql-cache/quicklatex.com-ee71dcb62c29bd1bdb33a867578c1746_l3.png) . (I did say that this should only work if we have to divide by
. (I did say that this should only work if we have to divide by